大哦：O（n）+ O（n）+ ... + O（n）如何等于O（n ^ 2）？

Question

我很难理解来自Algorithms by S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani - page 24的以下陈述，他们将O（n）的总和表示为O（n ² ）。但是我对O（n）的理解是n的线性函数，无论线性函数添加多少次（对于任何给定的n），它都不能是二次的。他们给出了如下的解释，例如13 x 11的二进制表示法。

        1 1 0 1
      x 1 0 1 1
      ----------
        1 1 0 1 (1101 times 1)
      1 1 0 1   (1101 times 1, shifted once)
    0 0 0 0     (1101 times 0, shifted twice)
+ 1 1 0 1       (1101 times 1, shifted thrice)
----------------
1 0 0 0 1 1 1 1 (binary 143)

  

如果x和y（这里是1101和1011）都是n位，那么那里   是n个中间行，有长度   最多2n位（采取移位   考虑到）。所花费的总时间   加上这些行，做两个数字   一次， O（n）+ O（n）+ ... +   O（n），即O（n ² ），二次方   输入的大小。

很抱歉，如果这很明显，但有人可以帮我理解为什么这是O（n ² ）？

Answer 1

如果 n 操作的复杂度为O（ n ），则总复杂度为 n ·O（ n ）即O（ n ² ）。

Answer 2

如果你做的事情需要N秒，并重复N次。完成需要多少秒？

N = 2 => 2*2 seconds.
N = 3 => 3*3 seconds.
N = 4 => 4*4 seconds.

      => N^2 seconds.

Answer 3

O（n）的东西不是O（n ² ）**如果它乘以常数因子。

n is O(n)  
7n is O(n)  
100000n is O(n)

n*n is O(n^2)

以下是来自维基百科的big-O的正式定义：

  

设f（x）和g（x）是两个函数   在真实的某个子集上定义   数字。一个人写道

     

     

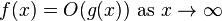
当且仅当，足够大   x，f（x）的值最多为a   常数乘以g（x）in   绝对值。也就是说，f（x）=   O（g（x））当且仅当存在时   正实数M和实数   数字x ₀ ，以便

     

** 警告：大O是上限。 O（n）的所有东西在技术上也是O（n ² ）。请参阅Big Theta和Big Omega。

http://en.wikipedia.org/wiki/Big_O_notation

Answer 4

当你说“任何给定的n”时，你会忘记当“给定的n” n本身时，那么你正在进行n次n（n）操作。那是 ² 。

Answer 5

如果你的操作是O（n）并且你做了n次，那就是O（n ^ 2）的定义。

您对O（n）操作的常数数量感到困惑，这些操作始终为O（n）。

在二进制乘法示例中，O（n）运算的数量取决于输入的长度，n。

Answer 6

O(n)次n次操作O(n^2)次O(n)次。如果n操作的数量线性地取决于输入大小O(n^2)，则会更严格，那么您将遇到{{1}}的情况。

Answer 7

这里的许多答案都忘记了重要的假设。如果你有n个操作，每个都是O（n）它不自动跟随总和是O（n ² ）！假设第k次操作需要k * n时间（因此它是常数n） - 第一次操作需要n次，第二次操作需要n * n等。然后前n次操作的总和为O（n ³ ）。

对于不相信者，这是一个来自CLRS的例子：

虚假声明：

 n
 Σ  k = O(n)
i=1

归纳证明：

对于n = 1,1 = O（1）。

对于n + 1，假设n适用假设，

n+1       n
 Σ  k = ( Σ k) + (n+1) =  O(n) + n = O(n)
i=1      i=1

“证明”是错误的，总和是O（n ² ）。

你只能说O（n）+ ... + O（n）是O（n ² ）如果隐藏在大O 中的常数都被一些人限制常数。在这种情况下，你可以写

O（n）+ ... + O（n）＆lt; = kn + kn + ... + kn＆lt; = kn ² = O（n ² ）。

如果常数没有限制，那就错了。

Answer 8

基本思想：因为隐藏在O（n）中的常数因子随着n的增加而增加，因此不是常数并且会产生矛盾。

Big-O表示法的一个缺点是它鼓励了诸如问题主题之类的误解。 O（n）+ O（n）建议你将线性函数类添加到自身，但它的真正含义是“任意两个线性函数之和的类”。总和再次是线性的，这很好，但结果恰好取决于只有两个（或任何常数）的求和线性函数。

因此，在上下文中，您的问题实际上意味着“为什么线性函数的数量增加的总和也不是线性的？”。证明草图非常简单：

'
- Assume, for simplicity, that all linear functions are of the form f(n) = c*n, c >= 1
- Suppose we have an increasing-as-N-increases set of summed linear functions
- Assume the sum of that set of functions is linear, ie. of the form c*n
  - Try to find a value of c that works for all values of N
  - But, for any c that works for N=x, it will fail for N=x+1 because there is another addition
  - Contradiction
- The sum of the set of functions is not linear

Answer 9

你必须添加两个n号码（花费O（n）时间），n次。 n（O（n））= O（n * n）= O（n ^ 2）。

Answer 10

答案很简单：

O（n）+ O（n）+···+ O（n） = X（n）

如果X是常数并且不随输入而改变，那么它仍然是O（n）。