3DпјҶпјғ34;е…Қиҙ№пјҶпјғ34;дёүи§’жөӢйҮҸзӣёжңә
жҲ‘еҫҲжҠұжӯүпјҢеҰӮжһңд№ӢеүҚжңүдәәжҸҗеҮәиҝҷдёӘй—®йўҳпјҢжҲ‘дјҡиҝӣиЎҢжҗңзҙўпјҢдҪҶжҲ‘жүҫдёҚеҲ°зӯ”жЎҲгҖӮ
жҲ‘зҡ„й—®йўҳжҳҜпјҢжҲ‘еёҢжңӣеңЁзӣёжңәзҡ„Xе’ҢYж—ӢиҪ¬зӣёе…ізҡ„жүҖжңү3дёӘиҪҙдёҠиҝӣиЎҢ移еҠЁгҖӮ
иҝҷе°ұжҳҜжҲ‘жүҖеҒҡзҡ„пјҡ
private static void fly(int addX, int addY){ //parameters are the direction change relative to the current rotation
float angleX = rotation.x + addX; //angle is basically the direction, into which we will be moving(when moving forward this is always the same as our actual rotation, therefore addX and addY would be 0, 0)
float angleY = rotation.y + addY;
float speed = (moveSpeed * 0.0002f) * delta;
float hypotenuse = speed; //the length that is SUPPOSED TO BE moved overall on all 3 axes
/* Y-Z side*/
//Hypotenuse, Adjacent and Opposite side lengths of a triangle on the Y-Z side
//The point where the Hypotenuse and the Adjacent meet is where the player currently is.
//OppYZ is the opposite of this triangle, which is the ammount that should be moved on the Y axis.
//the Adjacent is not used, don't get confused by it. I just put it there, so it looks nicer.
float HypYZ = speed;
float AdjYZ = (float) (HypYZ * Math.cos(Math.toRadians(angleX))); //adjacent is on the Z axis
float OppYZ = (float) (HypYZ * Math.sin(Math.toRadians(angleX))); //opposite is on the Y axis
/* X-Z side*/
//Side lengths of a triangle on the Y-Z side
//The point where the Hypotenuse and the Adjacent meet is where the player currently is.
float HypXZ = speed;
float AdjXZ = (float) (HypXZ * Math.cos(Math.toRadians(angleY))); //on X
float OppXZ = (float) (HypXZ * Math.sin(Math.toRadians(angleY))); //on Z
position.x += AdjXZ;
position.y += OppYZ;
position.z += OppXZ;
}
жҲ‘еҸӘеңЁеүҚиҝӣпјҲеҸӮж•°пјҡ0,90пјүжҲ–еҗ‘еҗҺпјҲеҸӮж•°пјҡ180,270пјүж—¶е®һзҺ°жӯӨж–№жі•пјҢеӣ дёәеңЁжЁӘеҗ‘移еҠЁж—¶YиҪҙдёҠдёҚдјҡеҸ‘з”ҹ移еҠЁпјҢеӣ дёәдҪ дёҚиғҪеңЁZиҪҙгҖӮ пјҲжЁӘеҗ‘移еҠЁзҡ„ж–№жі•пјҲжү«е°„пјүе·ҘдҪңеҫ—еҫҲеҘҪпјҢжүҖд»ҘжҲ‘дёҚдјҡж·»еҠ е®ғгҖӮпјү
й—®йўҳжҳҜпјҢеҪ“жҲ‘еҗ‘дёҠзңӢ90еәҰжҲ–еҗ‘дёӢзңӢ90еәҰ然еҗҺеҗ‘еүҚ移еҠЁж—¶жҲ‘еә”иҜҘеҸӘеңЁYиҪҙдёҠ移еҠЁпјҲеһӮзӣҙпјүдҪҶжҳҜз”ұдәҺжҹҗз§ҚеҺҹеӣ жҲ‘д№ҹеҗ‘еүҚ移еҠЁпјҲиҝҷж„Ҹе‘ізқҖеңЁZдёҠпјүиҪҙпјҢеӣ дёәXиҪҙжҳҜжү«е°„пјүгҖӮ
жҲ‘зЎ®е®һж„ҸиҜҶеҲ°иҝҷз§Қ移еҠЁйҖҹеәҰ并дёҚжҳҜдёҖжҲҗдёҚеҸҳзҡ„гҖӮеҰӮжһңдҪ жңүи§ЈеҶіж–№жЎҲпјҢжҲ‘д№ҹеҫҲд№җж„ҸжҺҘеҸ—е®ғгҖӮ
1 дёӘзӯ”жЎҲ:
зӯ”жЎҲ 0 :(еҫ—еҲҶпјҡ5)
жҲ‘и®ӨдёәдҪ зҡ„й”ҷиҜҜеңЁдәҺдҪ жІЎжңүе®Ңе…ЁжҠ•е°„дҪ зҡ„и·қзҰ»пјҲдҪ зҡ„移еҠЁйҮҸhypothenuseпјүеңЁж°ҙе№ійқўе’ҢеһӮзӣҙе№ійқўдёҠгҖӮ
жҚўеҸҘиҜқиҜҙпјҢж— и®әйҖүжӢ©е“ӘдёӘж–№еҗ‘пјҢдҪ зҺ°еңЁжӯЈеңЁеҒҡзҡ„жҳҜеңЁж°ҙе№ійқўXZдёӯ移еҠЁдҪ зҡ„hypothenuseзӮ№пјҢеҚідҪҝдҪ е·Із»Ҹ移еҠЁдәҶhypothenuseзҡ„дёҖйғЁеҲҶеһӮзӣҙж–№еҗ‘YгҖӮ
жӮЁеҸҜиғҪжғіиҰҒеҒҡзҡ„жҳҜе°Ҷhypothenuseж•°йҮҸдҪңдёәжҖ»ж•°гҖӮ
еӣ жӯӨпјҢжӮЁеҝ…йЎ»иҜ„дј°еңЁж°ҙе№іе№ійқўдёӯеҸ‘з”ҹдәҶеӨҡе°‘иҝҗеҠЁд»ҘеҸҠеңЁеһӮзӣҙиҪҙдёҠиҝӣиЎҢдәҶеӨҡе°‘иҝҗеҠЁгҖӮдҪ зҡ„ж–№еҗ‘з»ҷдҪ зӯ”жЎҲгҖӮ
зҺ°еңЁпјҢжҲ‘зҺ°еңЁиҝҳдёҚжё…жҘҡдҪ зҡ„дёӨдёӘи§’еәҰд»ЈиЎЁд»Җд№ҲгҖӮжҲ‘ејәзғҲе»әи®®жӮЁеңЁиҝҷз§Қжғ…еҶөдёӢдҪҝз”ЁTaitвҖ“Bryan anglesпјҲд»…дҪҝз”Ё yawn е’Ңйҹій«ҳпјҢеӣ дёәжӮЁдјјд№ҺдёҚйңҖиҰҒж»ҡеҠЁ - дҪ з§°д№ӢдёәZж—ӢиҪ¬пјүпјҢд»Ҙз®ҖеҢ–и®Ўз®—гҖӮ
еңЁжӯӨй…ҚзҪ®дёӯпјҢе“Ҳж¬ и§’жҳҺжҳҫдёҺжӮЁеҜ№angleYзҡ„е®ҡд№үзӣёдјјпјҢиҖҢдҝҜд»°и§’еҲҷжҳҜж°ҙе№ійқўдёҺhypothenuseзҹўйҮҸд№Ӣй—ҙзҡ„и§’еәҰпјҲиҖҢдёҚжҳҜи§’еәҰпјүеңЁYZе№ійқўдёҠзҡ„жҠ•еҪұгҖӮ
иҰҒйҳҗжҳҺзҡ„жһ¶жһ„пјҡ
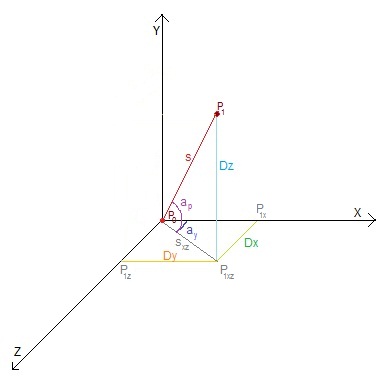
дҪҝз”Ёпјҡ
-
sд»ҺеҲқе§ӢдҪҚзҪ®P_0еҲ°P_1пјҲhypothenuseпјү зҡ„移еҠЁйҮҸ
-
a_yе“Ҳж¬ и§’е’Ңa_pжҠ•зҗғ -
D_xпјҢD_yпјҢD_zжҜҸдёӘиҪҙзҡ„дҪҚ移пјҲе°Ҷж·»еҠ еҲ°positionпјҢеҚіAdjXZпјҢOppYZе’Ң{ {1}}пјү
еӣ жӯӨпјҢеҰӮжһңжӮЁжҹҘзңӢжӯӨиЎЁзӨәпјҢжӮЁеҸҜд»ҘзңӢеҲ°X-Zдёӯзҡ„дёүи§’еҪўжІЎжңүOppXZдҪңдёәж–ңиҫ№дҪҶжҳҜе…¶жҠ•еҪұsгҖӮеҜ№жӯӨи·қзҰ»зҡ„иҜ„дј°йқһеёёз®ҖеҚ•пјҡеҰӮжһңжӮЁе°ҶиҮӘе·ұзҪ®дәҺдёүи§’еҪўs_xz P_0 P_1дёӯпјҢеҲҷеҸҜд»ҘзңӢеҲ°P_1xzгҖӮиҝҷз»ҷдәҶдҪ пјҡ
s_xz = s * cos(a_p)иҮідәҺfloat HypXZ = speed * Math.cos(Math.toRadians(angleP))); // s_xz
float AdjXZ = (float) (HypXZ * Math.cos(Math.toRadians(angleY))); // D_x
float OppXZ = (float) (HypXZ * Math.sin(Math.toRadians(angleY))); // D_z
еҚіD_yпјҢиҜ·еҶҚж¬Ўе°ҶиҮӘе·ұж”ҫеңЁдёүи§’еҪўOppYZ P_0 P_1дёӯпјҢ然еҗҺжӮЁе°ҶиҺ·еҫ—пјҡ
P_1xzзҺ°еңЁпјҢеҰӮжһңfloat OppYZ = (float) (speed * Math.sin(Math.toRadians(angleP))); // D_y
жҢүз…§жҲ‘зҡ„еҒҮи®ҫдҪ е®һйҷ…дёҠж„Ҹе‘ізқҖжҸҗеҚҮзҡ„и§’еәҰпјҢйӮЈд№Ҳд»Јз Ғдёӯзҡ„angleXе’ҢangleP = angleXгҖӮ
йҖҡиҝҮжӯӨжӣҙжӯЈпјҢеҰӮжһңHypXZ = AdjYZжҲ–angleX = 90пјҢеҲҷ
angleX = -90 ...еӣ жӯӨHypXZ = speed * cos(angleX) = speed * cos(90deg) = speed * 0;
е’ҢAdjXZ = 0гҖӮеңЁж°ҙе№ійқўдёҠжІЎжңү移еҠЁгҖӮ
жіЁж„Ҹпјҡ
иҰҒжЈҖжҹҘжӮЁзҡ„и®Ўз®—жҳҜеҗҰжӯЈзЎ®пјҢжӮЁеҸҜд»ҘйӘҢиҜҒжӮЁжҳҜеҗҰзЎ®е®һ移еҠЁдәҶжүҖйңҖ移еҠЁйҮҸзҡ„зӮ№пјҲOppXZ = 0пјҢеҚіhypothenuseпјҢеҚіspeedпјүгҖӮдҪҝз”ЁжҜ•иҫҫе“ҘжӢүж–Ҝе®ҡзҗҶпјҡ
sж №жҚ®дёҠйқўз»ҷеҮәзҡ„дҪҚ移е®ҡд№үпјҡ
sВІ = s_xzВІ + D_zВІ // Applied in the triangle P_0 P_1 P_1xz
= D_xВІ + D_yВІ + D_zВІ // Applied in the triangle P_0 P_1x P_1xz
еёҢжңӣе®ғжңүжүҖеё®еҠ©......еҶҚи§ҒпјҒ
- з»ҷе®ҡж‘„еғҸжңәе’Ңи§Ҷеӣҫе№ійқўзҡ„2DзӮ№зҡ„3Dеқҗж Ү
- и®Ўз®—зӮ№зҡ„3Dж—ӢиҪ¬
- дёүи§’еӯҰ3dж•°еӯҰ第дёүдәәз§°зӣёжңәз®—жі•
- 3DпјҶпјғ34;е…Қиҙ№пјҶпјғ34;дёүи§’жөӢйҮҸзӣёжңә
- дҪҝз”Ёйј ж Ү移еҠЁж—ӢиҪ¬3Dи§Ҷеӣҫ - дҪҝз”Ёеӣәе®ҡж‘„еғҸеӨҙ
- OpenGLзӣёжңә/ж–№еҗ‘зҹўйҮҸ
- д»Һз»ҷе®ҡзҡ„еҪ’дёҖеҢ–ж–№еҗ‘еҗ‘йҮҸзҡ„3Dж—ӢиҪ¬пјҹ
- 3DзҹўйҮҸеұҸ幕角еәҰ
- еҰӮдҪ•е°Ҷиҝҷдәӣ3Dзӣёжңәдёүи§’еҪўж–№зЁӢиҪ¬жҚўдёәеңЁж–°иҪҙдёҠе·ҘдҪң
- е…·жңүж°ҙе№і/еһӮзӣҙи§’еәҰзҡ„3Dзӣёжңә-йқўеҜ№дёҖдёӘзӮ№
- жҲ‘еҶҷдәҶиҝҷж®өд»Јз ҒпјҢдҪҶжҲ‘ж— жі•зҗҶи§ЈжҲ‘зҡ„й”ҷиҜҜ
- жҲ‘ж— жі•д»ҺдёҖдёӘд»Јз Ғе®һдҫӢзҡ„еҲ—иЎЁдёӯеҲ йҷӨ None еҖјпјҢдҪҶжҲ‘еҸҜд»ҘеңЁеҸҰдёҖдёӘе®һдҫӢдёӯгҖӮдёәд»Җд№Ҳе®ғйҖӮз”ЁдәҺдёҖдёӘз»ҶеҲҶеёӮеңәиҖҢдёҚйҖӮз”ЁдәҺеҸҰдёҖдёӘз»ҶеҲҶеёӮеңәпјҹ
- жҳҜеҗҰжңүеҸҜиғҪдҪҝ loadstring дёҚеҸҜиғҪзӯүдәҺжү“еҚ°пјҹеҚўйҳҝ
- javaдёӯзҡ„random.expovariate()
- Appscript йҖҡиҝҮдјҡи®®еңЁ Google ж—ҘеҺҶдёӯеҸ‘йҖҒз”өеӯҗйӮ®д»¶е’ҢеҲӣе»әжҙ»еҠЁ
- дёәд»Җд№ҲжҲ‘зҡ„ Onclick з®ӯеӨҙеҠҹиғҪеңЁ React дёӯдёҚиө·дҪңз”Ёпјҹ
- еңЁжӯӨд»Јз ҒдёӯжҳҜеҗҰжңүдҪҝз”ЁвҖңthisвҖқзҡ„жӣҝд»Јж–№жі•пјҹ
- еңЁ SQL Server е’Ң PostgreSQL дёҠжҹҘиҜўпјҢжҲ‘еҰӮдҪ•д»Һ第дёҖдёӘиЎЁиҺ·еҫ—第дәҢдёӘиЎЁзҡ„еҸҜи§ҶеҢ–
- жҜҸеҚғдёӘж•°еӯ—еҫ—еҲ°
- жӣҙж–°дәҶеҹҺеёӮиҫ№з•Ң KML ж–Ү件зҡ„жқҘжәҗпјҹ