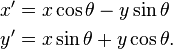用于旋转原点周围点的正确三角法

Question

以下哪种方法都使用正确的数学来旋转一个点？如果是这样，哪一个是正确的？

POINT rotate_point(float cx,float cy,float angle,POINT p)
{
  float s = sin(angle);
  float c = cos(angle);

  // translate point back to origin:
  p.x -= cx;
  p.y -= cy;

  // Which One Is Correct:
  // This?
  float xnew = p.x * c - p.y * s;
  float ynew = p.x * s + p.y * c;
  // Or This?
  float xnew = p.x * c + p.y * s;
  float ynew = -p.x * s + p.y * c;

  // translate point back:
  p.x = xnew + cx;
  p.y = ynew + cy;
}

Answer 1

From Wikipedia

要使用矩阵进行旋转，将要旋转的点（x，y）写为矢量，然后乘以从角度θ计算的矩阵，如下所示：

其中（x'，y'）是旋转后点的坐标，x'和y'的公式可以看作是

Answer 2

这取决于您如何定义angle。如果它是逆时针测量的（这是数学约定）那么正确的旋转是你的第一个：

// This?
float xnew = p.x * c - p.y * s;
float ynew = p.x * s + p.y * c;

但如果按顺时针方向测量，那么第二个是正确的：

// Or This?
float xnew = p.x * c + p.y * s;
float ynew = -p.x * s + p.y * c;

Answer 3

这是从我自己的矢量库中提取的。

//----------------------------------------------------------------------------------
// Returns clockwise-rotated vector, using given angle and centered at vector
//----------------------------------------------------------------------------------
CVector2D   CVector2D::RotateVector(float fThetaRadian, const CVector2D& vector) const
{
    // Basically still similar operation with rotation on origin
    // except we treat given rotation center (vector) as our origin now
    float fNewX = this->X - vector.X;
    float fNewY = this->Y - vector.Y;

    CVector2D vectorRes(    cosf(fThetaRadian)* fNewX - sinf(fThetaRadian)* fNewY,
                            sinf(fThetaRadian)* fNewX + cosf(fThetaRadian)* fNewY);
    vectorRes += vector;
    return vectorRes;
}