将3D坐标投影到具有已知点的2D图像上

Question

我正在编写一个.NET程序，允许用户通过识别图像上的特定点来注册图像，然后指定与每个点相关联的真实世界坐标。

http://www.ironbyte.ca/temp/mountain.jpg

图像注册过程还要求用户指定相机的坐标。

注册图像后我想要做的就是根据实际坐标在图像上绘制其他点。

我已经完成了很多关于观点预测的阅读，但我正在努力让事情发挥作用。我必须承认，我的数学技能不是他们应该成为斗争的一部分。我遇到的问题是试图确定焦距和显示器表面的距离：

在本文中称为查看者的位置（e [x，y，z]）：http://en.wikipedia.org/wiki/3D_projection#Perspective_projection

我也一直在提到这篇文章： http://www.shotlink.com/Tour/WebTemplate/shotlinknew.nsf/2c47cc31e412bc4985256e6e00287832/c1743b40acf6aa03852575b7007122b0/$FILE/Plotting%203D%20ShotLink%20Data%20on%202D%20Images.pdf 它从视野中提取焦距，这似乎是事先知道的，但不是我的情况。

所以我想我的问题是，有没有办法可以反过来根据我图像上已知点的位置来确定焦距和/或视野？或者我是以错误的方式看待这一点，也许有一种更简单的方法来实现最终目标？

Answer 1

---

编辑： 我对模式中的混合单元感到困惑。我因此重新做了一些答案。

---

如果我们看一下投影背后的数学，那对我来说听起来是可行的。

这是水平坐标的情况不太严格的模式（我混合现实世界坐标和像素一来试图说明你的情况）：

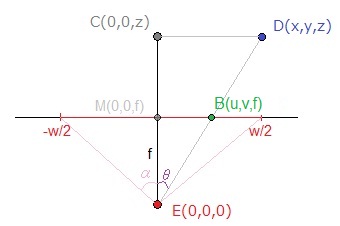
使用：

• D，用户给出的一个点，(x,y,z)其投影位置与相机定义的相对坐标系相关（因此在应用其平移和旋转后）
• E摄像机点 - 上述坐标系的原点。
• B图片平面中的结果点，以u和v为单位。图片平面的尺寸为w x h像素。
• f焦距（与x相同的单位，y，z ...） ，以像素为单位< / em>， F它在真实世界单元中的值，α水平半角视图 - 您要评估的值

---

您可以看到三角形 ECD 和 EBM 类似，因此使用Side-Splitter Theorem，我们得到：

• EM / EC = MB / CD＆lt; =＆gt; f / z = u / x（我们正在比较比率，所以如果等式的左边成员使用真实世界单位而右边的成员使用像素 ，则没有问题是真实世界值除以像素）

我们得到：

• f = u / x * z

现在，如果你想要 α F ，我想你需要知道尺寸r_x x {{ 1}}（真实世界单位）相机的传感器，因为：

• r_y tan(α) = (r_x / 2) / f

但至于F = r_x / (w / 2) * f，你可以通过：

• α

---

如果你想与你所指出的维基百科文章并行，我们一直在使用：

其中：

• tan(α) = (w / 2) / f = (d_x,d_y,d_z)，相机系统中该点的位置
• (x,y,z) = (s_x,s_y)，可打印表面的大小
• (w,h) = (r_x,r_y,r_z)，记录表面的特征
• (r_x,r_y,f) = (b_x,b_y)，在您的可打印表面上的位置

Answer 2

我能够使用Tsai算法（http://en.wikipedia.org/wiki/Camera_resectioning#Algorithms）的实现来解决这个问题，该算法可以使用最少4个已知点来计算投影矩阵。基本上，我允许用户指定点的世界坐标，然后单击图像以指定图像坐标。该算法使用这些映射（映射越多，解决方案越准确），以及图像宽度和高度来计算投影矩阵。然后可以使用该投影矩阵使用世界坐标将附加点投影到图像上。