е…·жңүnдёӘйғЁеҲҶзҡ„еӨҡе°‘дёӘдёҚеҗҢеҲҶеҢәеҸҜд»Ҙз”ұе…·жңүkдёӘе…ғзҙ зҡ„йӣҶеҗҲз»„жҲҗпјҹ
еҸҜд»ҘдҪҝз”ЁйӣҶеҗҲ{1,2,3,4}еҲ¶дҪңеӨҡе°‘дёӘе…·жңүдёӨдёӘйғЁеҲҶзҡ„дёҚеҗҢеҲҶеҢәпјҹ жӯӨеҲ—иЎЁдёӯжңү4дёӘе…ғзҙ йңҖиҰҒеҲҶдёә2дёӘйғЁеҲҶгҖӮжҲ‘еҶҷдәҶиҝҷдәӣпјҢжҖ»е…ұжңү7з§ҚдёҚеҗҢзҡ„еҸҜиғҪжҖ§пјҡ
- {{1}пјҢ{2,3,4}}
- {{2}пјҢ{1,3,4}}
- {{3}пјҢ{1,2,4}}
- {{4}пјҢ{1,2,3}}
- {{1,2}пјҢ{3,4}}
- {{1,3}пјҢ{2,4}}
- {{1,4}пјҢ{2,3}}
зҺ°еңЁжҲ‘еҝ…йЎ»дёәйӣҶеҗҲ{1,2,3пјҢ...пјҢ100}еӣһзӯ”зӣёеҗҢзҡ„й—®йўҳгҖӮ жӯӨеҲ—иЎЁдёӯжңү100дёӘе…ғзҙ йңҖиҰҒеҲҶдёә2дёӘйғЁеҲҶгҖӮжҲ‘зҹҘйҒ“еҲҶеҢәзҡ„дёҖйғЁеҲҶжңҖеӨ§еҸҜд»ҘжҳҜ50пјҲеҚі100/2пјүпјҢжңҖе°Ҹзҡ„жҳҜ1пјҲеӣ жӯӨдёҖйғЁеҲҶжңү1дёӘж•°еӯ—иҖҢеҸҰдёҖйғЁеҲҶжңү99пјүгҖӮеҰӮдҪ•еңЁдёҚеҶҷеҮәжҜҸдёӘеҸҜиғҪз»„еҗҲзҡ„ж— е…іеҲ—иЎЁзҡ„жғ…еҶөдёӢпјҢзЎ®е®ҡдёӨдёӘйғЁеҲҶзҡ„еҲҶеҢәжңүеӨҡе°‘з§ҚдёҚеҗҢзҡ„еҸҜиғҪжҖ§пјҹ зӯ”жЎҲеҸҜд»Ҙз®ҖеҢ–дёәйҳ¶д№ҳпјҲдҫӢеҰӮ12пјҒпјүеҗ—пјҹ жҳҜеҗҰжңүдёҖдёӘйҖҡз”Ёе…¬ејҸеҸҜд»Ҙз”ЁжқҘжҹҘжүҫе…·жңүnдёӘйғЁеҲҶзҡ„еӨҡе°‘дёӘдёҚеҗҢзҡ„еҲҶеҢәеҸҜд»Ҙз”ұе…·жңүkдёӘе…ғзҙ зҡ„йӣҶеҗҲз»„жҲҗпјҹ
2 дёӘзӯ”жЎҲ:
зӯ”жЎҲ 0 :(еҫ—еҲҶпјҡ6)
1пјүstackoverflowжҳҜе…ідәҺзј–зЁӢзҡ„гҖӮжӮЁзҡ„й—®йўҳеұһдәҺhttps://math.stackexchange.com/йўҶеҹҹгҖӮ
2пјүдёҖз»„nдёӘе…ғзҙ дёӯжңү2дёӘ n еӯҗйӣҶпјҲеӣ дёәnдёӘе…ғзҙ дёӯзҡ„жҜҸдёҖдёӘеҸҜд»ҘеҢ…еҗ«еңЁзү№е®ҡеӯҗйӣҶдёӯпјҢд№ҹеҸҜд»ҘдёҚеҢ…еҗ«еңЁзү№е®ҡеӯҗйӣҶдёӯпјүгҖӮиҝҷз»ҷдәҶжҲ‘们2дёӘ n-1 nе…ғзҙ йӣҶзҡ„дёҚеҗҢеҲҶеҢәеҲ°дёӨдёӘеӯҗйӣҶдёӯгҖӮе…¶дёӯдёҖдёӘеҲҶеҢәжҳҜеҫ®дёҚи¶ійҒ“зҡ„пјҲе…¶дёӯдёҖдёӘйғЁеҲҶжҳҜдёҖдёӘз©әеӯҗйӣҶпјҢеҸҰдёҖдёӘйғЁеҲҶжҳҜж•ҙдёӘеҺҹе§ӢйӣҶеҗҲпјүпјҢд»ҺжӮЁзҡ„зӨәдҫӢдёӯзңӢиө·жқҘжӮЁдјјд№ҺдёҚжғіи®Ўз®—жҷ®йҖҡеҲҶеҢәгҖӮжүҖд»Ҙзӯ”жЎҲжҳҜ2 n-1 -1пјҲеҜ№дәҺn = 4пјҢе®ғз»ҷеҮә2 3 -1 = 7пјүгҖӮ
зӯ”жЎҲ 1 :(еҫ—еҲҶпјҡ1)
nдёӘйғЁеҲҶе’ҢkдёӘе…ғзҙ зҡ„дёҖиҲ¬зӯ”жЎҲжҳҜthe Stirling number of the second kind S(k,n)гҖӮ
иҜ·жіЁж„ҸпјҢйҖҡеёёзҡ„жғҜдҫӢжҳҜnе…ғзҙ жҖ»ж•°пјҢеӣ жӯӨSпјҲnпјҢkпјү
и®Ўз®—йҖҡз”Ёе…¬ејҸйқһеёёйҡҫзңӢпјҢдҪҶk = 2еҸҜиЎҢпјҲдҪҝз”ЁйҖҡз”Ёз¬ҰеҸ·пјүпјҡ
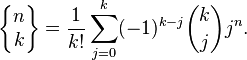
еӣ жӯӨSпјҲnпјҢ2пјү= 1/2пјҲпјҲ+1пјү* 1 * 0 n +пјҲ - 1пјү* 2 * 1 n +пјҲ +1пјү* 1 * 2 n пјү=пјҲ0-2 + 2 n пјү/ 2 = 2 n-1 - 1
- жҹҘжүҫе…·жңүkдёӘеӨ§е°Ҹзҡ„еӯҗйӣҶзҡ„nдёӘе…ғзҙ зҡ„жүҖжңүеҸҜиғҪеҲҶеҢәпјҢе…¶дёӯдёӨдёӘе…ғзҙ д»…е…ұдә«зӣёеҗҢзҡ„дёҖж¬Ў
- жһҡдёҫе…·жңүNдёӘе…ғзҙ зҡ„1dж•°з»„зҡ„жүҖжңүkеҲҶеҢәпјҹ
- е…·жңүnдёӘйғЁеҲҶзҡ„еӨҡе°‘дёӘдёҚеҗҢеҲҶеҢәеҸҜд»Ҙз”ұе…·жңүkдёӘе…ғзҙ зҡ„йӣҶеҗҲз»„жҲҗпјҹ
- жһҡдёҫжүҖжңүnдҪҚж•ҙж•°пјҢе…¶дёӯkдҪҚи®ҫзҪ®дёә1
- sort -kпјғгҖӮпјғnдёҚеҗҢдәҺsort -kпјғгҖӮпјғ - nпјҹ
- е…·жңүжңҖе°Ҹе’ҢжңҖеӨ§йӣ¶д»¶еҖјзҡ„kйӣ¶д»¶зҡ„еҲҶеҢә
- nеҲҶдёәkйғЁеҲҶжңүйҷҗеҲ¶
- жқҘиҮӘйӣҶеҗҲN haskellзҡ„kдёӘе…ғзҙ зҡ„з»„еҗҲ
- е°Ҷе…·жңүnдёӘе…ғзҙ зҡ„йӣҶеҗҲзҡ„еҲҶеҢәж•°и®Ўж•°дёәkдёӘеӯҗйӣҶ
- зҪ‘ж јN * MдёҠжңүеӨҡе°‘дёӘзҹ©еҪўжӯЈеҘҪеҢ…еҗ«kдёӘзҹ©еҪў
- жҲ‘еҶҷдәҶиҝҷж®өд»Јз ҒпјҢдҪҶжҲ‘ж— жі•зҗҶи§ЈжҲ‘зҡ„й”ҷиҜҜ
- жҲ‘ж— жі•д»ҺдёҖдёӘд»Јз Ғе®һдҫӢзҡ„еҲ—иЎЁдёӯеҲ йҷӨ None еҖјпјҢдҪҶжҲ‘еҸҜд»ҘеңЁеҸҰдёҖдёӘе®һдҫӢдёӯгҖӮдёәд»Җд№Ҳе®ғйҖӮз”ЁдәҺдёҖдёӘз»ҶеҲҶеёӮеңәиҖҢдёҚйҖӮз”ЁдәҺеҸҰдёҖдёӘз»ҶеҲҶеёӮеңәпјҹ
- жҳҜеҗҰжңүеҸҜиғҪдҪҝ loadstring дёҚеҸҜиғҪзӯүдәҺжү“еҚ°пјҹеҚўйҳҝ
- javaдёӯзҡ„random.expovariate()
- Appscript йҖҡиҝҮдјҡи®®еңЁ Google ж—ҘеҺҶдёӯеҸ‘йҖҒз”өеӯҗйӮ®д»¶е’ҢеҲӣе»әжҙ»еҠЁ
- дёәд»Җд№ҲжҲ‘зҡ„ Onclick з®ӯеӨҙеҠҹиғҪеңЁ React дёӯдёҚиө·дҪңз”Ёпјҹ
- еңЁжӯӨд»Јз ҒдёӯжҳҜеҗҰжңүдҪҝз”ЁвҖңthisвҖқзҡ„жӣҝд»Јж–№жі•пјҹ
- еңЁ SQL Server е’Ң PostgreSQL дёҠжҹҘиҜўпјҢжҲ‘еҰӮдҪ•д»Һ第дёҖдёӘиЎЁиҺ·еҫ—第дәҢдёӘиЎЁзҡ„еҸҜи§ҶеҢ–
- жҜҸеҚғдёӘж•°еӯ—еҫ—еҲ°
- жӣҙж–°дәҶеҹҺеёӮиҫ№з•Ң KML ж–Ү件зҡ„жқҘжәҗпјҹ