如何计算椭圆的轴对齐边界框？

时间：2008-09-17 21:13:52

标签： math graphics geometry

如果椭圆的长轴是垂直的或水平的，那么很容易计算边界框，但椭圆旋转的时候呢？

到目前为止，我能想到的唯一方法是计算周边的所有点并找到最大/最小x和y值。似乎应该有一种更简单的方法。

如果有一个函数（在数学意义上）描述一个任意角度的椭圆，那么我可以用它的导数找到斜率为零或未定义的点，但我似乎找不到一个。 / p>

编辑：为了澄清，我需要轴对齐的边界框，即它不应该与椭圆一起旋转，而是保持与x轴对齐，因此转换边界框将不起作用。

11 个答案:

答案 0 :(得分：35)

您可以尝试将参数化方程用于以任意角度旋转的椭圆：

x = h + a*cos(t)*cos(phi) - b*sin(t)*sin(phi)  [1]
y = k + b*sin(t)*cos(phi) + a*cos(t)*sin(phi)  [2]

...其中椭圆具有中心（h，k）半长轴a和半轴b，并且通过角度phi旋转。

然后您可以区分并求解gradient = 0：

0 = dx/dt = -a*sin(t)*cos(phi) - b*cos(t)*sin(phi)

=＆GT; 

tan(t) = -b*tan(phi)/a   [3]

哪个应该为你提供很多解决方案（其中两个你感兴趣），将其插回[1]以获得你的最大和最小x。

重复[2]：

0 = dy/dt = b*cos(t)*cos(phi) - a*sin(t)*sin(phi)

=＆GT; 

tan(t) = b*cot(phi)/a  [4]

让我们举个例子：

在（0,0）处考虑椭圆，a = 2，b = 1，按PI / 4旋转：

[1] =＆gt; 

x = 2*cos(t)*cos(PI/4) - sin(t)*sin(PI/4)

[3] =＆gt; 

tan(t) = -tan(PI/4)/2 = -1/2

=＆GT; 

t = -0.4636 + n*PI

我们感兴趣的是t = -0.4636和t = -3.6052

所以我们得到：

x = 2*cos(-0.4636)*cos(PI/4) - sin(-0.4636)*sin(PI/4) = 1.5811

和

x = 2*cos(-3.6052)*cos(PI/4) - sin(-3.6052)*sin(PI/4) = -1.5811

答案 1 :(得分：8)

我在http://www.iquilezles.org/www/articles/ellipses/ellipses.htm找到了一个简单的公式（忽略了z轴）。

我大致这样实现了它：

num ux = ellipse.r1 * cos(ellipse.phi);
num uy = ellipse.r1 * sin(ellipse.phi);
num vx = ellipse.r2 * cos(ellipse.phi+PI/2);
num vy = ellipse.r2 * sin(ellipse.phi+PI/2);

num bbox_halfwidth = sqrt(ux*ux + vx*vx);
num bbox_halfheight = sqrt(uy*uy + vy*vy); 

Point bbox_ul_corner = new Point(ellipse.center.x - bbox_halfwidth, 
                                 ellipse.center.y - bbox_halfheight);

Point bbox_br_corner = new Point(ellipse.center.x + bbox_halfwidth, 
                                 ellipse.center.y + bbox_halfheight);

答案 2 :(得分：6)

这是相对简单但有点难以解释，因为你没有给我们你代表椭圆的方式。有很多方法可以做到这一点..

无论如何，一般原则是这样的：你不能直接计算轴对齐的边界框。但是，您可以将x和y中椭圆的极值计算为2D空间中的点。

为此，取方程x（t）= ellipse_equation（t）和y（t）= ellipse_equation（t）就足够了。获取它的第一个阶导数，并为它的根解决它。因为我们正在处理基于三角函数的椭圆，这是直截了当的。你应该得到一个方程式，通过atan，acos或asin得到根。

提示：要检查你的代码，请尝试使用未旋转的椭圆：你应该得到0，Pi / 2，Pi和3 * Pi / 2的根。

对每个轴（x和y）执行此操作。您将获得最多四个根（如果您的椭圆退化，则更少，例如，其中一个半径为零）。评估根部的位置，得到椭圆的所有极值点。

现在你快到了。获取椭圆的边界框就像扫描这四个点的xmin，xmax，ymin和ymax一样简单。

顺便说一下 - 如果你在找到椭圆方程时遇到问题：尝试将它缩小到你的轴对齐椭圆，中心，两个半径和围绕中心的旋转角度。

如果这样做，方程式变为：

  // the ellipse unrotated:
  temp_x (t) = radius.x * cos(t);
  temp_y (t) = radius.y = sin(t);

  // the ellipse with rotation applied:
  x(t) = temp_x(t) * cos(angle) - temp_y(t) * sin(angle) + center.x;
  y(t) = temp_x(t) * sin(angle) + temp_y(t) * cos(angle) + center.y;

答案 3 :(得分：4)

Brilian Johan Nilsson。 我已将您的代码转录为c＃ - ellipseAngle现在是度数：

private static RectangleF EllipseBoundingBox(int ellipseCenterX, int ellipseCenterY, int ellipseRadiusX, int ellipseRadiusY, double ellipseAngle)
{
    double angle = ellipseAngle * Math.PI / 180;
    double a = ellipseRadiusX * Math.Cos(angle);
    double b = ellipseRadiusY * Math.Sin(angle);
    double c = ellipseRadiusX * Math.Sin(angle);
    double d = ellipseRadiusY * Math.Cos(angle);
    double width = Math.Sqrt(Math.Pow(a, 2) + Math.Pow(b, 2)) * 2;
    double height = Math.Sqrt(Math.Pow(c, 2) + Math.Pow(d, 2)) * 2;
    var x= ellipseCenterX - width * 0.5;
    var y= ellipseCenterY + height * 0.5;
    return new Rectangle((int)x, (int)y, (int)width, (int)height);
}

答案 4 :(得分：2)

我认为最有用的公式就是这个。从原点的角度phi旋转的省略号具有等式：

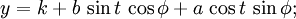
alt text

alt text

其中（h，k）是中心，a和b是长轴和短轴的大小，t从-pi到pi变化。

由此，你应该能够推导出t dx / dt或dy / dt为0。

答案 5 :(得分：1)

如果椭圆由其焦点和偏心率给出，则为以下情况的公式（对于由轴长度，中心和角度给出的情况，请参见例如用户1789690的答案）

即，如果焦点是（x0，y0）和（x1，y1）并且偏心率是e，那么

bbox_halfwidth  = sqrt(k2*dx2 + (k2-1)*dy2)/2
bbox_halfheight = sqrt((k2-1)*dx2 + k2*dy2)/2

，其中

dx = x1-x0
dy = y1-y0
dx2 = dx*dx
dy2 = dy*dy
k2 = 1.0/(e*e)

我从用户1789690和Johan Nilsson的答案中得出了公式。

答案 6 :(得分：1)

如果您使用OpenCV / C ++并使用cv::fitEllipse(..)函数，则可能需要使用椭圆的矩形。在这里，我使用迈克的答案做了一个解决方案：

// tau = 2 * pi, see tau manifest
const double TAU = 2 * std::acos(-1);

cv::Rect calcEllipseBoundingBox(const cv::RotatedRect &anEllipse)
{
    if (std::fmod(std::abs(anEllipse.angle), 90.0) <= 0.01) {
        return anEllipse.boundingRect();
    }

    double phi   = anEllipse.angle * TAU / 360;
    double major = anEllipse.size.width  / 2.0;
    double minor = anEllipse.size.height / 2.0;

    if (minor > major) {
        std::swap(minor, major);
        phi += TAU / 4;
    }

    double cosPhi = std::cos(phi), sinPhi = std::sin(phi);
    double tanPhi = sinPhi / cosPhi;

    double tx = std::atan(-minor * tanPhi / major);
    cv::Vec2d eqx{ major * cosPhi, - minor * sinPhi };
    double x1 = eqx.dot({ std::cos(tx),           std::sin(tx)           });
    double x2 = eqx.dot({ std::cos(tx + TAU / 2), std::sin(tx + TAU / 2) });

    double ty = std::atan(minor / (major * tanPhi));
    cv::Vec2d eqy{ major * sinPhi, minor * cosPhi };
    double y1 = eqy.dot({ std::cos(ty),           std::sin(ty)           });
    double y2 = eqy.dot({ std::cos(ty + TAU / 2), std::sin(ty + TAU / 2) });

    cv::Rect_<float> bb{
        cv::Point2f(std::min(x1, x2), std::min(y1, y2)),
        cv::Point2f(std::max(x1, x2), std::max(y1, y2))
    };

    return bb + anEllipse.center;
}

答案 7 :(得分：0)

此代码基于上面提供的代码user1789690，但在Delphi中实现。我测试了这个，据我所知它完美无缺。我花了一整天时间搜索算法或一些代码，测试了一些不起作用的代码，我很高兴终于找到了上面的代码。我希望有人觉得这很有用。此代码将计算旋转椭圆的边界框。边界框是轴对齐的，不随椭圆旋转。半径是旋转前的椭圆。

type

  TSingleRect = record
    X:      Single;
    Y:      Single;
    Width:  Single;
    Height: Single;
  end;

function GetBoundingBoxForRotatedEllipse(EllipseCenterX, EllipseCenterY, EllipseRadiusX,  EllipseRadiusY, EllipseAngle: Single): TSingleRect;
var
  a: Single;
  b: Single;
  c: Single;
  d: Single;
begin
  a := EllipseRadiusX * Cos(EllipseAngle);
  b := EllipseRadiusY * Sin(EllipseAngle);
  c := EllipseRadiusX * Sin(EllipseAngle);
  d := EllipseRadiusY * Cos(EllipseAngle);
  Result.Width  := Hypot(a, b) * 2;
  Result.Height := Hypot(c, d) * 2;
  Result.X      := EllipseCenterX - Result.Width * 0.5;
  Result.Y      := EllipseCenterY - Result.Height * 0.5;
end;

答案 8 :(得分：0)

这是我的功能，用于找到任意方向的椭圆形紧密拟合矩形

我有opencv rect并指出实现：

cg - 椭圆的中心

尺寸 - 椭圆的主要短轴

角度 - 椭圆的方向

cv::Rect ellipse_bounding_box(const cv::Point2f &cg, const cv::Size2f &size, const float angle) {

    float a = size.width / 2;
    float b = size.height / 2;
    cv::Point pts[4];

    float phi = angle * (CV_PI / 180);
    float tan_angle = tan(phi);
    float t = atan((-b*tan_angle) / a);
    float x = cg.x + a*cos(t)*cos(phi) - b*sin(t)*sin(phi);
    float y = cg.y + b*sin(t)*cos(phi) + a*cos(t)*sin(phi);
    pts[0] = cv::Point(cvRound(x), cvRound(y));

    t = atan((b*(1 / tan(phi))) / a);
    x = cg.x + a*cos(t)*cos(phi) - b*sin(t)*sin(phi);
    y = cg.y + b*sin(t)*cos(phi) + a*cos(t)*sin(phi);
    pts[1] = cv::Point(cvRound(x), cvRound(y));

    phi += CV_PI;
    tan_angle = tan(phi);
    t = atan((-b*tan_angle) / a);
    x = cg.x + a*cos(t)*cos(phi) - b*sin(t)*sin(phi);
    y = cg.y + b*sin(t)*cos(phi) + a*cos(t)*sin(phi);
    pts[2] = cv::Point(cvRound(x), cvRound(y));

    t = atan((b*(1 / tan(phi))) / a);
    x = cg.x + a*cos(t)*cos(phi) - b*sin(t)*sin(phi);
    y = cg.y + b*sin(t)*cos(phi) + a*cos(t)*sin(phi);
    pts[3] = cv::Point(cvRound(x), cvRound(y));

    long left = 0xfffffff, top = 0xfffffff, right = 0, bottom = 0;
    for (int i = 0; i < 4; i++) {
        left = left < pts[i].x ? left : pts[i].x;
        top = top < pts[i].y ? top : pts[i].y;
        right = right > pts[i].x ? right : pts[i].x;
        bottom = bottom > pts[i].y ? bottom : pts[i].y;
    }
    cv::Rect fit_rect(left, top, (right - left) + 1, (bottom - top) + 1);
    return fit_rect;
}

答案 9 :(得分：0)

这是一个在 javascript 中围绕旋转椭圆的边界框的简单示例： https://jsfiddle.net/rkn61mjL/1/

这个想法非常简单，不需要复杂的计算和求解梯度：

  1. 计算一个简单的非旋转椭圆的边界框：

    let p1 = [centerX - radiusX, centerY - radiusY];
let p2 = [centerX + radiusX, centerY - radiusY];
let p3 = [centerX + radiusX, centerY + radiusY];
let p4 = [centerX - radiusX, centerY + radiusY];

  2. 围绕椭圆中心旋转所有四个点：

    p1 = [(p1[0]-centerX) * Math.cos(radians) - (p1[1]-centerY) *  Math.sin(radians) + centerX,
    (p1[0]-centerX) * Math.sin(radians) + (p1[1]-centerY) * Math.cos(radians) + centerY];        
p2 = [(p2[0]-centerX) * Math.cos(radians) - (p2[1]-centerY) *  Math.sin(radians) + centerX,
    (p2[0]-centerX) * Math.sin(radians) + (p2[1]-centerY) * Math.cos(radians) + centerY];        
p3 = [(p3[0]-centerX) * Math.cos(radians) - (p3[1]-centerY) *  Math.sin(radians) + centerX,
    (p3[0]-centerX) * Math.sin(radians) + (p3[1]-centerY) * Math.cos(radians) + centerY];        
p4 = [(p4[0]-centerX) * Math.cos(radians) - (p4[1]-centerY) *  Math.sin(radians) + centerX,
    (p4[0]-centerX) * Math.sin(radians) + (p4[1]-centerY) * Math.cos(radians) + centerY];

答案 10 :(得分：0)

这是基于上述答案的打字稿函数。

import discord 
from discord.ext import commands 
  client = commands.Bot(command_prefix = "+")
  @client.event
  async def on_ready():
    print('Bot is ready')
  @client.event    
  async def on_member_join(member):
    print(f'{member}has joined the server')
  @client.event  
  async def on_member_remove(member):
    print(f'{member}has left the server')  


client.run('token')
相关问题
最新问题