线性规划 - 约束

Question

我正在尝试将此（项目的一小部分）编码为线性编程：

对于每个包p，我们知道它的长度（xDimp）和宽度（yDimp）。另外，我们有卡车的长度（xTruck）和宽度（yTruck）。所有数字都是整数。

由于包装的设计，放在卡车上时不能旋转。

卡车表示为2维矩阵，仅用x和y坐标表示。我们忽略了身高。

决策变量：

- pxy [p，x，y] =包p在具有右上坐标（x，y）的单元格中

- pbl [p，x，y] = p的左下角单元格有右上角坐标（x，y）

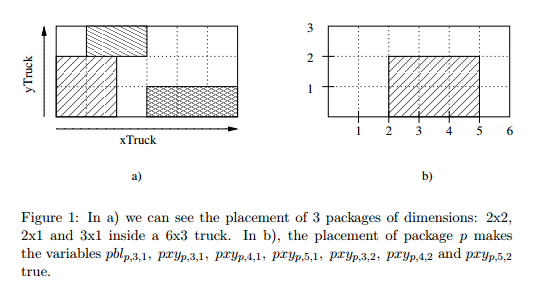
如何编写这样的约束来设置pbl和pxy变量？我说我应该设置变量pbl以确保包装适合卡车，pxy变量的值取决于pbl的值。

谢谢，

Answer 1

这是垃圾箱包装问题的变体，是在封闭矩形（2BP）中具有不同宽度和高度的多个矩形的二维包装。如果它们只允许旋转90°，我们就会得到正交方向矩形填充问题，在您的情况下，我们有一个不可旋转的矩形填充问题。它的计算复杂性是NP难的，但并不是不可行的。 根据您的描述，问题已经被分离，限制了可能的网格布局，这意味着连续版本的最佳可能不再可用。

一个approch是预先计算某些冲突图，它代表你的搜索空间并保存有关矩形重叠的信息：

其中

每条边都代表冲突，每个节点代表卡车内的可能位置。两个包p和q与iff

相交

和成对。

现在，网格上的打包问题是冲突图（MIS）上的最大独立设置问题，假设您想要最大化卡车上的包数。反过来，MIS具有以下ILP公式：

这是MIS的整数松弛，但仍不适用于分支定界求解方法。如果 C 是 G 中的clique，则任何独立集都可以从 C 中选择最多一个节点，因此使用以下约束：

得到的线性程序的变量数呈指数增长。

为了更进一步，您可以尝试元约束满足方法。 首先，使用以下约束来确保您的包裹在卡车内：

其次，使用一组析取约束来防止重叠：

从那时起，您可以开始制定元程序，如描述here

我认为这应该足够开始:-) 您可以在有关组合优化的文献中找到更多信息。

  

来源：

     

http://www.staff.uni-mainz.de/schoemer/publications/ESA03.pdf

     

https://kluedo.ub.uni-kl.de/frontdoor/index/index/docId/2046