距离矩阵的近似估计

Question

我有一组N个对象，我想计算一个NxN距离矩阵。有时我的N个对象的集合非常大，我想通过仅计算距离比较的子集来计算NxN距离矩阵的近似值。

有人能指出我计算全距离矩阵近似值的方向吗？我有一些想法，但我想避免重新发明轮子。

编辑：算法类型的一个例子将利用如下事实：如果对象A和对象B之间的距离非常小，并且对象B和对象C之间的距离非常小，则必须物体A和C之间的距离略短。

Answer 1

您的“对象”是否在网络上？如果对象在网络中，您可以使用this或this来生成所有对最短路径。如果没有，我认为你很难计算所有的n x n距离。

Answer 2

老实说，我认为这取决于你想要近似的距离以及你的子集有多大。如果您只是想要了解矩阵的外观，您可以对随机子集（包括最大和最小节点）进行简单的线性插值，从而得到非常准确（tm）的结果。

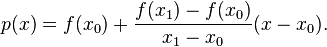
我认为这里真正的技巧是找出启发式（线性，二次等插值）和子集大小。您还可以计算出各种子集的距离矩阵，然后用某种方法（线性，球形线性，立方）对这些矩阵进行插值。

根据您的初始样本，它几乎是一个启发式试验和错误，直到您“噢，这足以满足我的需求”。

Answer 3

您需要的解决方案类似于我们在图表中常见的解决方案，您可以使用All pair shortest path来查找距离，还可以查看johnson's algorithm

Answer 4

我遇到了同样的问题，最终为它编写了Python代码：

https://github.com/jpeterbaker/lazyDistance

README.md说明了如何使用三角形不等式更新每个距离的上限和下限。

只需在二维空间中将Python文件作为脚本运行作为示例。绘制的线是唯一实际计算出的距离。

在我的版本中，节省时间并不是要拥有大量对象。正如我所写的那样，它是O（n ^ 4）算法，因此，如果对象的数量很大，它比仅计算所有距离实际上更糟糕。但是，当对象数量较少时，我的方法将节省时间，并且距离函数的计算成本非常高。假定执行多个O（n ^ 2）运算要比进行单个距离测量更快。

如果n大，则可以寻找更便宜的方法来确定下一个要计算的距离（不涉及距离边界矩阵的n ^ 2个项的算术运算）。您也可能不需要每次执行此代码时都更新所有2 * n ^ 2边界。