Question

我正在尝试找到一个具有适度空间要求的快速算法来解决以下问题。

对于DAG的每个顶点，在DAG的传递闭包中找到其度数和出度的总和。

鉴于此DAG：

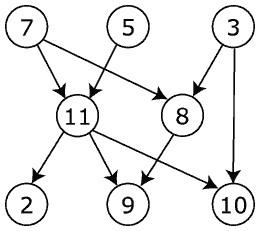
DAG from Wikipedia

我希望得到以下结果：

Vertex #   Reacability Count  Reachable Vertices in closure
   7             5            (11, 8, 2, 9, 10)
   5             4            (11, 2, 9, 10)
   3             3            (8, 9, 10)
  11             5            (7, 5, 2, 9, 10)
   8             3            (7, 3, 9)
   2             3            (7, 5, 11)
   9             5            (7, 5, 11, 8, 3)
  10             4            (7, 5, 11, 3)

在我看来，如果不实际构建传递闭包，这应该是可能的。我无法在网上找到任何确切描述此问题的内容。我对如何做到这一点有一些想法，但我想知道SO人群能想出什么。

Answer 1

OMG，它错了！ SORRY！

我会把它留下来，直到找到一个好的替代方案。如果可能的话，CW-ed可以随意讨论和扩展。

使用动态编程。

for each vertex V
   count[V] = UNKNOWN
for each vertex V
   getCount(V)


function getCount(V)
   if count[V] == UNKNOWN
      count[V] = 0
      for each edge (V, V2)
        count[V] += getCount(V2) + 1          
   return count[V]

这是带有邻接列表的O(|V|+|E|)。它只计算传递闭包中的外度。要计算in-degrees，请在边缘反转的情况下调用getCount。要获得总和，请将两次调用的计数相加。

要了解这是O(|V|+|E|)的原因，请考虑以下事项：每个顶点V将完全1 + in-degree(V)次访问：一次直接访问V，一次访问每一个边{ {1}}。在后续访问中，(*, V)只会在getCount(V)中返回已记忆的count[V]。

另一种看待它的方法是计算每条边的跟随次数：恰好一次。

Answer 2

对于每个节点，使用BFS或DFS查找out-reachability。

再次针对反方向再次找到可达性。

时间复杂度：O（MN + N ²），空间复杂度：O（M + N）。

Answer 3

对于一个确切的答案，我认为很难击败KennyTM的算法。如果您愿意接受近似值，那么坦克计数方法（http://www.guardian.co.uk/world/2006/jul/20/secondworldwar.tvandradio）可能有所帮助。

为每个顶点分配一个[0,1]范围内的随机数。使用像polygenelubricants这样的线性时间动态程序来计算每个顶点v从v可到达的最小数量minreach（v）。然后估计从v可到达的顶点数量为1 / minreach（v） - 1.为了更好的准确性，重复几次并在每个顶点取一个中位数。

Answer 4

我已经为这个问题构建了一个可行的解决方案。我的解决方案基于topological sorting算法的修改。下面的算法只计算传递闭包中的in-degree。 out-degree可以以相同的方式计算，边缘反转，每个顶点的两个计数相加，以确定最终的“可达性计数”。

for each vertex V
   inCount[V] = inDegree(V)   // inDegree() is O(1)
   if inCount[V] == 0
      pending.addTail(V)

while pending not empty
   process(pending.removeHead())

function process(V)
   for each edge (V, V2)
      predecessors[V2].add(predecessors[V])   // probably O(|predecessors[V]|)
      predecessors[V2].add(V)
      inCount[V2] -= 1
      if inCount[V2] == 0
          pending.add(V2)
   count[V] = sizeof(predecessors[V])         // store final answer for V
   predecessors[V] = EMPTY                    // save some memory

假设设置操作为O（1），则该算法在O（| V | + | E |）中运行。但是，更有可能的是，集合联合操作predecessors[V2].add(predecessors[V])使其更糟糕。设定联合所需的附加步骤取决于DAG的形状。我相信最坏的情况是O（| V | ^ 2 + | E |）。在我的测试中，这个算法表现出比我迄今为止尝试过的任何其他算法更好的性能。

此外，通过为完全处理的顶点处理前驱集，该算法通常比大多数替代使用更少的内存。但是，上述算法的最坏情况内存消耗与构造传递闭包的情况相匹配，但对于大多数DAG而言，情况并非如此。

Answer 5

我假设您有一个所有顶点的列表，并且每个顶点都有一个id和一个可以直接从它到达的顶点列表。

然后，您可以添加另一个字段（或者您表示的那个），该字段包含您也可以间接到达的顶点。我会在递归深度优先搜索中执行此操作，在各个到达节点的字段中记住结果。作为这种数据结构，您可能会使用某种树，它可以有效地删除重复项。

可以通过添加反向链接单独完成in-reachability，但是也可以通过累积当前的out-reach节点并将它们添加到相应的字段来完成与out-reacability相同的传递。到达节点。

Answer 6

我相信解决此问题的方法是简单的动态编程。

保持reach [v]中从节点v可达的顶点数。然后，reach [v] = Sum（reach [child_k [v]]）。对于叶子，您初始化reach [v] = 1。

要确定伸手可及的距离，请反转边缘的方向并进行相同的操作。

要使动态规划能够在线性时间和空间中进行计算，您需要以DAG的反向拓扑顺序计算可达性[v]。

最终复杂度：O（V + E）。

查找DAG的所有顶点的可达性计数

6 个答案:

OMG，它错了！ SORRY！