如何计算负加速度？

时间：2010-02-19 18:49:13

标签： user-interface math physics touchscreen

我正在实现触摸屏用户界面的滚动行为，但是我现在太累了，无法将我的想法包围在一些所谓的微不足道的数学中：

y (distance/velocity)
|********
|        ******
|              ****
|                  ***
|                     ***
|                        **
|                          **
|                            *
|                             *
-------------------------------- x (time)

F（X） - ＆GT;

UI应该允许用户在任何方向上拖动和“抛出”视图，并且即使在他从屏幕上释放手指之后也保持滚动一段时间。它的动量取决于用户在取下手指之前拖动的速度。

所以我有一个起始速度（v0），每20ms我滚动一个相对于当前速度的量。每次滚动迭代时，我都会降低速度，直到它停止时它低于阈值。当我将它减去固定量（线性）时，它看起来并不正确，所以我需要建模负加速度，但未能提出一个不错的简单公式如何计算我必须降低速度的量在每次迭代中。

更新

感谢您到目前为止的回复，但我仍然无法从反馈中获得令人满意的功能。我可能没有足够好地描述所需的解决方案，所以我将尝试给出一个真实世界的例子来说明我想要做什么样的计算：

假设在某条街道上有一辆汽车行驶，并且驾驶员踩刹车到最大值直到汽车停下来。司机多次在同一条街上用同一辆车做这件事，但开始以不同的速度制动。当汽车减速时，我希望能够仅仅根据当前的速度计算一秒钟后的速度。对于这种计算，当驾驶员开始破坏时，汽车行驶的速度无关紧要，因为所有环境因素都保持不变。当然，公式中会有一些常数，但是当汽车下降到30米/秒时，它将在下一秒内达到相同的距离，无论是否在驾驶员开始破坏时行驶100或50米/秒。因此，打中断后的时间也不是函数的参数。一定速度下的减速度总是一样的。

如果在减速，质量，摩擦或其他任何因素中忽略一些复杂的影响，如空气阻力，如何在这种情况下一秒钟后计算速度？我只是在动能之后，由于汽车的摩擦而消耗它。

更新2 我现在看到汽车的加速度将是liniear，这实际上不是我想要的。我会清理它并明天尝试新的建议。感谢您的推荐到目前为止。

15 个答案:

答案 0 :(得分：8)

[简答（假设C语法）] 

double v(double old_v, double dt) {
    t = t_for(old_v); 
    new_t = t - dt; 
    return (new_t <= 0)?0:v_for(t);
}

double t_for(double v)和double v_for(double t)是来自v-to-t双向映射（数学中的函数）的返回值，它是任意的，具有monothonic并为{{1}定义的约束（因此有一个点v >=0）。一个例子是：

v=0

哪里有：

  1. double v_for(double t) { return pow(t, k); } double t_for(double v) { return pow(v, 1.0/k); } 随着时间的推移减速度减去模数。
  2. k>1随着时间的推移减速度增加模数。
  3. k<1不断减速。

    4. [较长的一个（有理由和情节）]

    所以目标必须是：

    1. 要找到一个函数k=1，它取当前速度值v(t+dt)=f(v(t),dt)和时间点v并返回当前dt的速度（它不需要实际指定t+dt，因为t已知并作为参数提供，而v(t)只是时间增量。 换句话说，任务是实现具有特定属性的例程dt（见下文）。

    2. [请注意] 有问题的函数有一个有用的（和所需）属性，无论前一个速度的“历史”如何，都会返回相同的结果变化。这意味着，例如，如果一系列连续速度为[100,50,10,0]（对于起始速度double next_v(curr_v, dt);），任何大于此的其他序列将具有相同的“尾部”： [150,100,50,10,0]（对于起始速度v0=100）等。 换句话说，无论起始速度如何，所有速度 - 时间图都将有效相互之间的副本只是沿着时间轴偏移，每个都由它自己的值（参见下图，注意线v0=150和t=0.0之间的图形部分是相同的）

    3. 此外，加速度t=2.0必须是时间w(t)=dv(t)/dt的递减函数（为了视觉上令人愉悦和我们在此处建模的移动GUI对象的“直观”行为）。 / p>

      4. 提议的想法是：

      1. 首先，您选择具有所需属性的 单声速度函数 （在您的情况下，它会逐渐减小加速度，但如下例所示，它是更容易使用“加速”的）。 此函数也不能有上边界 ，因此您可以将其用于任何大的速度值。此外， 它必须有一个速度为零的点 。一些例子是：t（不完全是你的情况，因为减速v(t) = k*t在这里是常数），k（这个是好的，在v=sqrt(-t)区间定义）。

      2. 然后，对于任何给定的速度，你会在上面的函数图中找到具有此速度值的点（将有一个点，因为函数没有绑定，只有一个因为它是单声道的），所以通过时间delta朝向较小的速度值，从而获得下一个。迭代将逐渐（并且不可避免地）带到速度为零的点。

      3. 基本上都是这样， 甚至不需要产生一些“最终”公式，依赖于时间值或初始（非当前）速度消失，编程变得非常简单< / b> 的

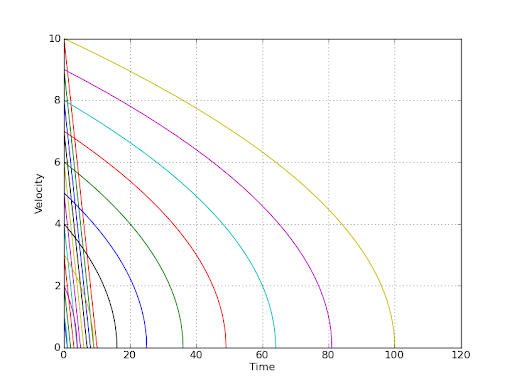
        4. 对于两个简单的情况，这个小的python脚本产生下面的图（给定的初始速度为t <= 0到1.0），并且，如您所见， 来自任何给定的速度“水平”和“向下”的情节“表现”相同 这是因为 无论你开始减速（减速）的速度，你都是“ “沿着相同的曲线移动相对于速度为（变为）零的点 ：

        10.0

        这给出了下面的图（线性减速（即恒定减速）的线性曲线，“曲线” - 对于“平方根”的情况（参见上面的代码））：

        另外请注意，要运行上面的脚本，需要安装 pylab，numpy 和朋友（但只有绘图部分，“核心”类依赖于什么，当然可以用于他们自己的。）

        P.S。通过这种方法，人们可以真正“构建”（例如，为不同的import numpy import pylab import math class VelocityCurve(object): """ An interface for the velocity 'curve'. Must represent a _monotonically_ _growing_ (i.e. with one-to-one correspondence between argument and value) function (think of a deceleration reverse-played) Must be defined for all larger-than-zero 'v' and 't' """ def v(self, t): raise NotImplementedError def t(self, v): raise NotImplementedError class VelocityValues(object): def __init__(self, v0, velocity_curve): assert v0 >= 0 assert velocity_curve self._v = v0 self._vc = velocity_curve def next_v(self, dt): t = self._vc.t(self._v) new_t = t - dt if new_t <= 0: self._v = 0 else: self._v = self._vc.v(new_t) return self._v class LinearVelocityCurve(VelocityCurve): def __init__(self, k): """k is for 'v(t)=k*t'""" super(LinearVelocityCurve, self).__init__() self._k = k def v(self, t): assert t >= 0 return self._k*t def t(self, v): assert v >= 0 return v/self._k class RootVelocityCurve(VelocityCurve): def __init__(self, k): """k is for 'v(t)=t^(1/k)'""" super(RootVelocityCurve, self).__init__() self._k = k def v(self, t): assert t >= 0 return math.pow(t, 1.0/self._k) def t(self, v): assert v >= 0 return math.pow(v, self._k) def plot_v_arr(v0, velocity_curve, dt): vel = VelocityValues(v0, velocity_curve) v_list = [v0] while True: v = vel.next_v(dt) v_list.append(v) if v <= 0: break v_arr = numpy.array(list(v_list)) t_arr = numpy.array(xrange(len(v_list)))*dt pylab.plot(t_arr, v_arr) dt = 0.1 for v0 in range(1, 11): plot_v_arr(v0, LinearVelocityCurve(1), dt) for v0 in range(1, 11): plot_v_arr(v0, RootVelocityCurve(2), dt) pylab.xlabel('Time ') pylab.ylabel('Velocity') pylab.grid(True) pylab.show() 间隔增加不同的功能，甚至平滑手绘（记录的）“人体工程学”曲线）他喜欢的“拖动”：）

答案 1 :(得分：5)

阅读评论后，我想改变我的回答： 将速度乘以k <1。 1，如k = 0.955，使其以指数方式衰减。

解释（带图表和可调方程！）跟随......

我将原始问题中的图解释为显示速度保持在起始值附近，然后逐渐减小。但是如果你想象一本书在桌子上滑动，它会迅速远离你，然后慢下来，然后滑行停止。我同意@Chris Farmer使用的正确模型是与速度成正比的阻力。我将采用这个模型并得出我上面建议的答案。我提前为这个问题道歉。我相信在数学上更好的人可以大大简化这一点。 另外，我直接链接到图表，SO解析器不喜欢的链接中有一些字符。 现在修复了网址。

我将使用以下定义：

x -> time
a(x) -> acceleration as a function of time
v(x) -> velocity as a function of time
y(x) -> position as a function of time
u -> constant coefficient of drag
colon : denotes proportionality

我们知道由于阻力引起的力与速度成正比。我们也知道力与加速度成正比。

a(x) : -u v(x)        (Eqn. 1)

减号确保加速度与当前行驶方向相反。

我们知道速度是综合加速度。

v(x) : integral( -u v(x) dx )        (Eqn. 2)

这意味着速度与其自身的积分成正比。我们知道e^x满足这个条件。所以我们假设

v(x) : e^(-u x)        (Eqn. 3)

指数中的阻力系数是这样的，当我们solve the integral in Eqn. 2时u取消回到Eqn。 3。

现在我们需要弄清楚u的价值。正如@BlueRaja指出的那样，e^x永远不会等于零，无论x。但是对于足够负的x，它接近于零。让我们考虑原始速度的1％被“停止”（你的阈值的想法），并且假设我们想要在x = 2秒内停止（你可以稍后调整它）。然后我们需要解决

e^(-2u) = 0.01        (Eqn. 4)

这导致我们计算

u = -ln(0.01)/2 ~= 2.3        (Eqn. 5)

Let's graph v(x)

看起来它在2秒内以指数方式衰减到一个小值。到目前为止，非常好。

我们不一定想在GUI中计算指数。我们知道我们可以轻松转换指数基数，

e^(-u x) = (e^-u)^x        (Eqn. 6)

我们也不想以秒为单位跟踪时间。我们知道我们的更新速率为20毫秒，所以让我们定义一个时间戳n，勾选率为50刻/秒。

n = 50 x        (Eqn. 7)

从Eqn代替u的值。 5成Eqn。 6，与Eqn相结合。 7，代入Eqn。 3，我们得到

v(n) : k^n, k = e^(ln(0.01)/2/50) ~= 0.955        (Eqn. 8)

Let's plot this with our new x-axis in timeticks.

同样，我们的速度函数与在所需迭代次数中衰减到1％的事物成比例，并遵循“在摩擦力的影响下滑行”模型。我们现在可以将我们的初始速度v0乘以等式。 8来获得任何时间步的实际速度n：

v(n) = v0 k^n        (Eqn. 9)

请注意，在实施中，没有必要跟踪v0！我们可以将封闭式v0 * k^n转换为递归，以获得最终答案 

v(n+1) = v(n)*k        (Eqn. 10)

这个答案满足了你不关心初始速度的约束 - 下一个速度总能用当前的速度来计算。

值得检查以确保位置行为有意义。这种速度模型之后的位置是

y(n) = y0 + sum(0..n)(v(n))        (Eqn. 11)

Eqn中的总和。 11是easily solved using the form of Eqn 9。使用索引变量p：

sum(p = 0..n-1)(v0 k^p) = v0 (1-k^n)/(1-k)        (Eqn. 12)

所以我们有

y(n) = y0 + v0 (1-k^n)/(1-k)        (Eqn. 13)

Let's plot this with y0 = 0 and v0 = 1.

所以我们看到一个快速离开原点，沿着优雅的海岸停下来。我相信这个图表比原始图表更加忠实地描述了滑动。

通常，您可以使用等式

调整k 
k = e^(ln(Threshold)/Time/Tickrate)        (Eqn. 14)
where:
Threshold is the fraction of starting velocity at which static friction kicks in
Time is the time in seconds at which the speed should drop to Threshold
Tickrate is your discrete sampling interval

（感谢@poke展示使用Wolfram Alpha绘制情节 - 非常甜蜜。）

OLD ANSWER

将速度乘以k <1。 1，如k = 0.98，使其以指数方式衰减。

答案 2 :(得分：4)

  

当汽车减速时，我希望能够仅根据当前的速度计算一秒钟之后的速度。

这将是加速度的定义。例如，如果加速度为a = -9 meters/sec/sec，而现在的速度为20 meters/sec，则从现在起1秒后，速度将为11 meters/sec。

换句话说，从现在开始到Δv秒之间的速度变化t（假设持续加速）将是

  

Δv = a*t

意味着任何时间t的速度的（经典物理学）方程，给定t=0处的初始速度（此速度称为v 0 ）

  

v(t) = v <子> 0 + a*t

使用您在微积分课程的前两周学到的知识，您还可以从上面的等式中得到x(t)（汽车在时间t的距离）的等式;这会给你

  

x(t) = x <子> 0 + v <子> 0 *t + 0.5*a*t 2

（也可以在没有微积分的情况下推导出这个，见here）

最后，如果你是为游戏做这个，而不是物理模拟（意味着你不需要精确的结果），你会想要简单地改变每一帧的位置和速度而不是每帧重新计算位置。为此，您需要在每帧执行以下操作，假设速度（和加速度）以像素/秒（-per-second）为单位测量：

velocity_new = velocity_old + acceleration/frames_per_second
position_new = position_old + velocity_old/frames_per_second

答案 3 :(得分：2)

好像你正在寻找随着时间的推移而增加的减速度。

尝试计算

Delta_v = -(A*t + B)，选择合适的常数A和B，适合你。

t是到那时为止的总时间。

通过添加Delta_v来更改您的速度。

这基本上对应于线性负加速度。

你基本上可以选择随时间增加的任何函数（比如f（t））

并计算

Delta_v = -f(t)

对f（t）的适当选择会给你你想要的效果。

您可以使用的一些示例：

f(t) = At + B.
f(t) = A*exp(Bt)

当然，你必须要玩一下并尝试找出正确的常数。

答案 4 :(得分：2)

每次迭代都可以将速度降低一个恒定的量。示例：您以50的速度开始，下一次迭代为40，然后是30,20,10，停止。这将代表一个恒定的“摩擦”，与速度无关，这实际上非常接近现实（见friction on Wikipedia）。

如果您不喜欢这种外观，则需要根据速度制作摩擦力。我认为线性关系friction = base-friction + (coefficient * velocity)，系数相当小就足够了。

答案 5 :(得分：2)

如果你想要在mtrw的回答评论中增加减速度，并且你对物理真实性不是很挑剔，下面的等式可能就是你想要的：

V（t + dt）= V（t） - K1 + K2 x V（t）

V（t）=当前速度 V（t + dt）=下一次增量的速度 K1和K2是您校准的常数。只需确保（K2 x Vmax）＆lt; K1，或者你会高速加速。

如果感觉不对，请尝试 V（t + dt）= V（t） - K1 + K2 x f（V（t））

其中f（x）是您选择的单调递增函数，可能是方形或平方根，具体取决于您想要感受的位置。只需确保（K2 x f（V（t）））＆lt; K1表示每个可能的V（t）。

（单调递增函数意味着当x增加时f（x）总是增加）

答案 6 :(得分：2)

我也会添加一个想法。看起来你不想要恒定（负）加速。这将产生如下等式：

v(t) = v(0) + a*t,

其中a是负加速度，t是时间，v(t)是时间t的速度。这给你：

v(t2) - v(t1) = a(t2-t1),

并且这意味着对于给定的Δt，速度差等于aΔt，常数。

您可能正在寻找的是“摩擦”术语，这取决于当前的速度。在这个假设下，速度变化率与当前速度成正比：

d v(t) / d t = -b*v(t).

解决上述问题很容易，你得到：v（t）= v（0）e -b t 。

对这个方程进行积分，得到x（t）= v（0）（1-e -b t ）/ b，其中x是位置。 v（0）= 1，b = 0.1的位置图 1 看起来像你可以使用的东西。使用b的值，并在等式中添加比例因子可能是您想要做的。

1 http://www.wolframalpha.com/input/?i=plot+%281+-+1+e^%28-0.1+x%29+%29+%2F+0.1+for+x+%3D+0+to+100

答案 7 :(得分：1)

速度的非线性变化意味着加速度不是恒定的。非恒定加速意味着系统受jerk的影响。取所有加速度方程式并加“（1/6）jt 3 ”。修复a，并给j一个小的负值，直到v达到0。

答案 8 :(得分：0)

你可以跟踪速度并每次将速度降低一小部分速度。我相信这会很好地模拟摩擦。

答案 9 :(得分：0)

acceleration = (force / mass) 
velocity = (acceleration * time)
(force from user's finger) = acceleration / mass = velocity / time
  1. 给视图一个质量（调整它直到事情看起来合理，然后让用户调整它）
  2. 识别一些新的力量（拖动）
  3. 给予新力（拖动）一个幅度（调整到合理，让用户调整它）
  4. 将新力施加到物体并观察它减速

答案 10 :(得分：0)

我会将速度降低为v = v * 0.9 然后我会有一个被认为是停止速度的速度。这样，对象最终会停下来，而不会继续消耗资源作为移动。 所以像 为（V = startingVelocity; V氮化1.0; V * = 0.9） { X + = V; }

答案 11 :(得分：0)

加速度是速度的一阶导数和距离的二阶导数。对于某些常数C和k，您的图形看起来像二阶抛物线，如C-k * x ^ 2。如果y确实是距离你需要a = -2k，如果y是速度你需要a = -2kx。在任何一种情况下，速度v（x）= V0 + a（x）* x。 （其中x实际上是时间。我遵循你的约定而不是使用t。）

答案 12 :(得分：0)

我试过这个，有效（在Ruby中）。不确定数学是否合理但输出看起来是正确的，这意味着当你走向中心时你会变得更快：

velocity=100;
(100.downto(0)).each { |distance_from_black_hole |  velocity=velocity+9.8/distance_from_black_hole; puts velocity; }

答案 13 :(得分：0)

关于汽车示例的一些非编程讨论。

首先，我假设驾驶员无法使刹车速度锁定。

大多数新驾驶员学习的第一件事（或者第二件或第三件事）是制动时的自然趋势是将制动踏板保持在固定位置。结果是当汽车从缓慢移动到停止时突然向前倾斜。发生这种情况是因为制动器正在从动态摩擦（其中制动力与制动压力成比例）转变为静摩擦力，其中制动力正在恢复汽车的前进动量。这种突然加速的跳跃是令人不快的，并且新驾驶员学会在减速结束时踩下踏板以停止。

这种行为掩盖了另一种僵化，但在手动变速器汽车的正常加速期间可以注意到这一点。当加速（或减速）时，如果驾驶员突然使变速器失去档位，所有乘客都会突然向前倾斜。实际发生的是，将他们压入座椅靠背的加速力突然被移除，然后他们重新回到中立的坐姿。更舒适的驾驶方式是逐渐拉动离合器，以便逐渐消除发动机的动力。

在这两种情况下，更美观的驾驶风格涉及平滑加速度，消除突然跳跃。这基本上是谈论连续二阶导数的另一种方式。几乎所有具有此属性的动作都是自然的。

答案 14 :(得分：0)

y(x) = y0 - a * e ^ ( k * x )

其中y0是起始常量，a和k是因素。

Example plot

相关问题
最新问题