еңЁPythonдёӯдҪҝз”ЁдҪҺйҖҡй»„жІ№иҝҮж»ӨеҷЁзҡ„Prolem
жҲ‘жғіиҝҮж»ӨпјҲдҪҺйҖҡпјүжҲ‘зҡ„дҝЎеҸ·пјҢеҪ“е®ғдёҚиө·дҪңз”Ёж—¶пјҢжҲ‘ејҖе§Ӣз ”з©¶дёәд»Җд№Ҳе®ғдёҚиө·дҪңз”ЁгҖӮ жҲ‘иҝӣиЎҢдәҶдёҖдәӣжөӢиҜ•пјҢжҲ‘еҜ№ButterworthиҝҮж»ӨеҷЁзҡ„жҖ§иғҪж„ҹеҲ°жңүдәӣжғҠ讶гҖӮ жҲ‘е·Із»ҸеңЁthis post
дёӯе®ҡд№үдәҶе®ғdef apply_filter(data, cutoff, fs, order=6, filter_type="low", analog=False):
nyq = 0.5 * fs
normalized_cutoff = cutoff / nyq
b,a = butter(order, normalized_cutoff, btype=filter_type, analog=analog, output="ba")
they = lfilter(b, a, data)
return(they)
еҰӮжһңжҲ‘йҮҮз”Ё1000дёӘе…ғзҙ й•ҝзҡ„ж ·жң¬пјҢе°ұеғҸиҝҷж ·
x = np.linspace(0, 2*np.pi, 1000)
y = np.sin(x) + 0.3* np.sin(10*x)
sampling_frequency = 1/ (x[-1] * 1e-3)
sampling_frequency
>> 159.15494309189532
# because i have 1000 thousand points for a "time" going up to 2 pi
plt.plot(x, y, x, apply_filter(y, cutoff=1, fs= sampling_frequency)
жҲ‘еҫ—еҲ°зҡ„
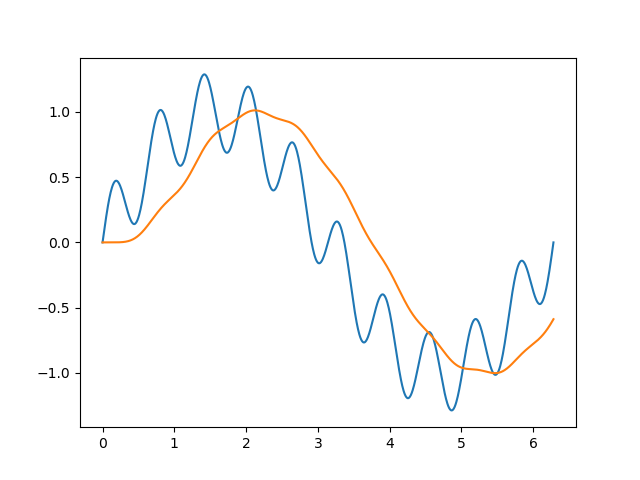
еҸҰдёҖж–№йқўпјҢеҰӮжһңжҲ‘еҒҡе®Ңе…ЁзӣёеҗҢзҡ„дәӢжғ…пјҢдҪҶжҳҜеҫ—еҲ°зҡ„еҲҶж•°дёҚеҗҢпјҢдҫӢеҰӮ10000пјҢжҲ‘еҫ—еҲ°зҡ„з»“жһңжҳҜй”ҷиҜҜзҡ„пјҢиҖҢдё”жҲ‘дёҚеӨӘжҳҺзҷҪдёәд»Җд№Ҳпјҡ
x = np.linspace(0, 2*np.pi, 10000)
y = np.sin(x) + 0.3* np.sin(10*x)
sampling_frequency = 1/ (x[-1] * 1e-4)
sampling_frequency
>> 1591.5494309189535
# because i have 10000 thousand points for a "time" going up to 2 pi
plt.plot(x, y, x, apply_filter(y, cutoff=1, fs= sampling_frequency)
иҝҷж¬ЎпјҢжҲ‘еҫ—еҲ°
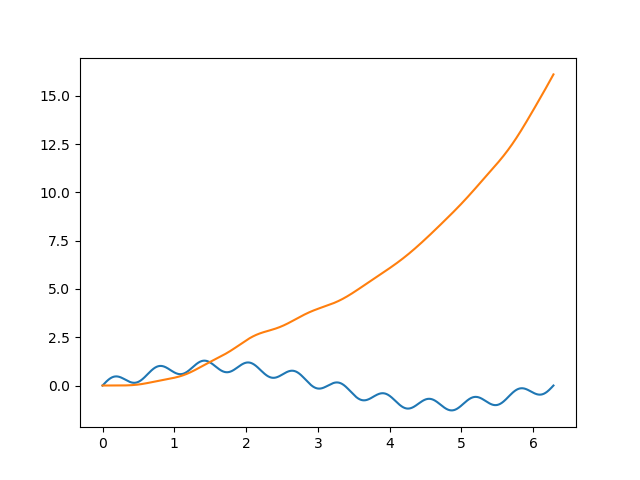
иҝҷжҳҫ然жҳҜй”ҷиҜҜзҡ„гҖӮ жңүдәәеҸҜд»Ҙи§ЈйҮҠдёәд»Җд№Ҳдјҡиҝҷж ·еҗ—пјҹдәӢжғ…дјјд№ҺеҸҜд»ҘжӯЈеёёиҝҗиЎҢ1000зӮ№жҲ–жӣҙе°‘...
зј–иҫ‘пјҡ
жҲ‘е·Із»Ҹз”»еҮәдәҶж»ӨжіўеҷЁзҡ„йў‘зҺҮе“Қеә”пјҢй—®йўҳеҮәеңЁиҝҷдәӣеӣҫиЎЁдёҠпјҢе°Ҫз®ЎжҲ‘д№ҹдёҚзҹҘйҒ“дёәд»Җд№Ҳдјҡиҝҷж ·еҒҡгҖӮ
sampling rate
>> 159.1549430918953
b, a = butter(6, 1/(sampling_rate/2))
w, h = freqz(b, a, 8000)
plt.subplot(2,1,1)
plt.xlim(0, 15)
plt.plot(0.5*sampling_rate*w/np.pi, np.abs(h))
жҲ‘еҫ—еҲ°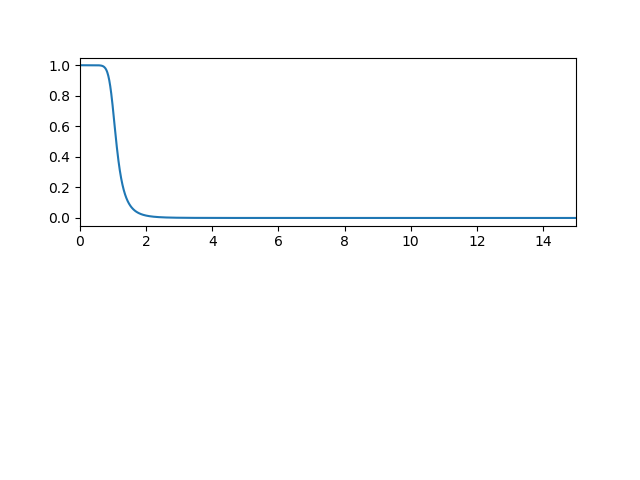
еҰӮжһңжҲ‘иҝҷж ·еҒҡ
sampling_frequency *= 10
sampling_frequency
>> 1591.5494309189535
b, a = butter(6, 1/(sampling_rate/2))
w, h = freqz(b, a, 8000)
plt.subplot(2,1,1)
plt.xlim(0, 15)
plt.plot(0.5*sampling_rate*w/np.pi, np.abs(h))
然еҗҺжҲ‘еҫ—еҲ°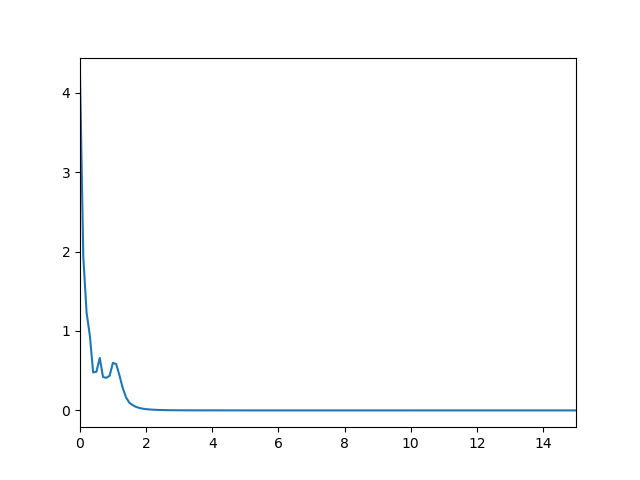
жҲ‘и§үеҫ—ButterworthеҮҪж•°еҸҜиғҪз”ұдәҺжҹҗдәӣеҺҹеӣ еңЁй«ҳеҲҶдёҠйҒҮеҲ°дәҶйә»зғҰпјҹ
ж„ҹи°ўжӮЁзҡ„её®еҠ©пјҒ
1 дёӘзӯ”жЎҲ:
зӯ”жЎҲ 0 :(еҫ—еҲҶпјҡ0)
еҜ№дәҺеҸҜиғҪж„ҹе…ҙи¶Јзҡ„дәәпјҢиҝҷе®һйҷ…дёҠжҳҜдёҺвҖң baвҖқиҫ“еҮәдёҖиө·дҪҝз”Ёзҡ„й»„жІ№иҝҮж»ӨеҷЁзҡ„вҖңе·ІзҹҘй—®йўҳвҖқгҖӮжӮЁеә”иҜҘж”№дёәдҪҝз”ЁвҖң zpkвҖқиҫ“еҮәпјҢиҜ·еҸӮи§Ғthis linkгҖӮ
жӮЁеҸҜд»Ҙд»Ҙйқһеёёз®ҖеҚ•зҡ„ж–№ејҸдҪҝз”ЁвҖң zpkвҖқиҫ“еҮәпјҢиҝҷдёҺдҪҝз”ЁвҖң baвҖқиҫ“еҮәйқһеёёзӣёдјјгҖӮиҝҷдјјд№ҺеҸҜд»Ҙе·ҘдҪңеӨҡиҫҫдёҖзҷҫдёҮзӮ№пјҢжІЎжңүзҗҶз”ұдёҚ继з»ӯе·ҘдҪңгҖӮ
иҝҷжҳҜдёҖдёӘеҹәжң¬зӨәдҫӢпјҡ
point_number=1000000
# our "data"
x = np.linspace(0, 2*np.pi, point_number)
y = sin(x) + 0.3* sin(10*x)
# sampling frequency would be 1/ sampling_time
sampling_frequency = point_number/(2*np.pi)
# hence the nyquist frequency
nyq = sampling_frequency/2
# desired cutoff frequency, in Hertz
cutoff = 1
# normalized for the function butter
normalized_cutoff = cutoff/nyq
z,p,k = butter(6, normalized_cutoff, output="zpk")
lesos = zpk2sos(z, p, k)
# filtered data
y_filtered_sos = sosfilt(lesos, y)
# plot part
plt.plot(x, y_filtered_sos, label="filtered data")
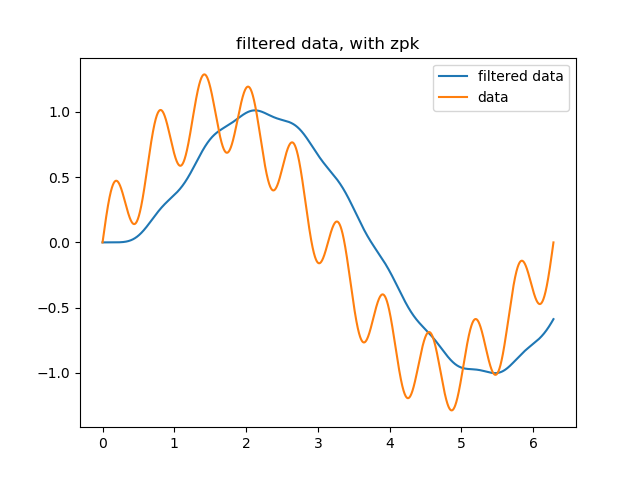
plt.title("filtered data, with zpk")
plt.plot(x,y, label="data")
plt.legend()
plt.title("filtered data, with zpk")
з»ҷеҮә
- е…·жңүfftwзҡ„зҗҶжғідҪҺйҖҡж»ӨжіўеҷЁ
- дҪҺйҖҡ然еҗҺPythonдёӯзҡ„еҸҚеҗ‘иҝҮж»ӨеҷЁ
- е…ідәҺеңЁMatlabдёӯдҪҝз”Ё'butter'еҮҪж•°зҡ„дҪҺйҖҡж»ӨжіўеҷЁзҡ„й—®йўҳ
- дҪҝз”ЁMatlabзј–з ҒеҷЁеҲӣе»әзӢ¬з«Ӣзҡ„й»„жІ№иҝҮж»ӨеҷЁ
- е…ідәҺPythonдёӯзҡ„иҝҮж»ӨеҷЁ
- дҪҝз”Ёй»„жІ№зҡ„ж•°еӯ—ж»ӨжіўеҷЁзі»ж•°
- еёҰдҪҺйҖҡж»ӨжіўеҷЁзҡ„ж»ӨжіўеҷЁеҠҹиғҪ
- еңЁPythonдёӯдҪҝз”ЁдҪҺйҖҡй»„жІ№иҝҮж»ӨеҷЁзҡ„Prolem
- дәҶи§ЈPythonдёӯзҡ„й»„жІ№д»·еҖјиҝҮж»ӨеҷЁ
- 2Dй»„жІ№еёҰйҖҡж»ӨжіўеҷЁпјҲз”ЁдәҺйҳөеҲ—пјү
- жҲ‘еҶҷдәҶиҝҷж®өд»Јз ҒпјҢдҪҶжҲ‘ж— жі•зҗҶи§ЈжҲ‘зҡ„й”ҷиҜҜ
- жҲ‘ж— жі•д»ҺдёҖдёӘд»Јз Ғе®һдҫӢзҡ„еҲ—иЎЁдёӯеҲ йҷӨ None еҖјпјҢдҪҶжҲ‘еҸҜд»ҘеңЁеҸҰдёҖдёӘе®һдҫӢдёӯгҖӮдёәд»Җд№Ҳе®ғйҖӮз”ЁдәҺдёҖдёӘз»ҶеҲҶеёӮеңәиҖҢдёҚйҖӮз”ЁдәҺеҸҰдёҖдёӘз»ҶеҲҶеёӮеңәпјҹ
- жҳҜеҗҰжңүеҸҜиғҪдҪҝ loadstring дёҚеҸҜиғҪзӯүдәҺжү“еҚ°пјҹеҚўйҳҝ
- javaдёӯзҡ„random.expovariate()
- Appscript йҖҡиҝҮдјҡи®®еңЁ Google ж—ҘеҺҶдёӯеҸ‘йҖҒз”өеӯҗйӮ®д»¶е’ҢеҲӣе»әжҙ»еҠЁ
- дёәд»Җд№ҲжҲ‘зҡ„ Onclick з®ӯеӨҙеҠҹиғҪеңЁ React дёӯдёҚиө·дҪңз”Ёпјҹ
- еңЁжӯӨд»Јз ҒдёӯжҳҜеҗҰжңүдҪҝз”ЁвҖңthisвҖқзҡ„жӣҝд»Јж–№жі•пјҹ
- еңЁ SQL Server е’Ң PostgreSQL дёҠжҹҘиҜўпјҢжҲ‘еҰӮдҪ•д»Һ第дёҖдёӘиЎЁиҺ·еҫ—第дәҢдёӘиЎЁзҡ„еҸҜи§ҶеҢ–
- жҜҸеҚғдёӘж•°еӯ—еҫ—еҲ°
- жӣҙж–°дәҶеҹҺеёӮиҫ№з•Ң KML ж–Ү件зҡ„жқҘжәҗпјҹ