样品分配模拟未达到正态

Question

我试图使用Python模拟“样本比例的样本分布”。我在示例here

中尝试了伯努利变量

问题在于，在大量的口香糖中，我们有黄色球的真实比例为0.6。如果我们取样（一定大小，例如10个），取其平均值并作图，我们应该得到正态分布。

我试图在python中做，但是我总是总是得到均匀的分布（或中间平坦）。我不明白我在想什么。

程序：

from SDSP import create_bernoulli_population, get_frequency_df
from random import shuffle, choices
from bi_to_nor_demo import get_metrics, bare_minimal_plot
import matplotlib.pyplot as plt


N = 10000  # 10000 balls
p = 0.6    # probability of yellow ball is 0.6, and others (1-0.6)=>0.4
n_pickups = 1000       # sample size
n_experiments = 100  # I dont know what this is called 


# generate population
population = create_bernoulli_population(N,p)
theor_df = get_frequency_df(population)
theor_df

# choose sample, take mean and add to X_mean_list. Do this for n_experiments times
X_hat = []
X_mean_list = []
for each_experiment in range(n_experiments):
    X_hat = choices(population, k=n_pickups)  # this method is with replacement
    shuffle(population)
    X_mean = sum(X_hat)/len(X_hat)
    X_mean_list.append(X_mean)

# plot X_mean_list as bar graph
stats_df = get_frequency_df(X_mean_list)
fig, ax = plt.subplots(1,1, figsize=(5,5))
X = stats_df['x'].tolist()
P = stats_df['p(x)'].tolist()    
ax.bar(X, P, color="C0") 

plt.show()

从属功能：
bi_to_nor_demo
SDSP

输出：

更新： 我什至尝试了如下所示的均匀分布，但是得到了相似的输出。不收敛于普通:(。（使用下面的函数代替create_bernoulli_population）

def create_uniform_population(N, Y=[]):
    """
    Given the total size of population N, 
    this function generates list of those outcomes uniformly distributed
    population list
    N - Population size, eg N=10000
    p - probability of interested outcome  
    Returns the outcomes spread out in population as a list
    """
    uniform_p = 1/len(Y)
    print(uniform_p)
    total_pops = []
    for i in range(0,len(Y)):
        each_o = [i]*(int(uniform_p*N))
        total_pops += each_o
    shuffle(total_pops)    
    return total_pops

Answer 1

能否请您分享matplotlib设置？我认为您已经将图截断了，这是正确的，因为beronulli上的样本比例的样本分布应该在总体期望值附近呈正态分布...

也许使用以下内容：

plt.tight_layout()

检查是否没有图形问题

Answer 2

def plotHist(nr, N, n_):
    ''' plots the RVs'''
    x = np.zeros((N))
    sp = f.add_subplot(3, 2, n_ )

    for i in range(N):    
        for j in range(nr):
            x[i] += np.random.binomial(10, 0.6)/10 
        x[i] *= 1/nr
    plt.hist(x, 100, normed=True, color='#348ABD', label=" %d RVs"%(nr));
    plt.setp(sp.get_yticklabels(), visible=False)


N = 1000000   # number of samples taken
nr = ([1, 2, 4, 8, 16, 32])

for i in range(np.size(nr)):
    plotHist(nr[i], N, i+1)

以上是基于我在CLT上写的一个普通博客的代码示例：https://rajeshrinet.github.io/blog/2014/central-limit-theorem/

从本质上讲，我正在从（0,1）范围内的分布生成几个随机数（nr）并将它们求和。然后我看到，随着我增加随机数的数量，它们如何收敛。

Here is a screenshot of the code and the result.

Answer 3

解决方案：
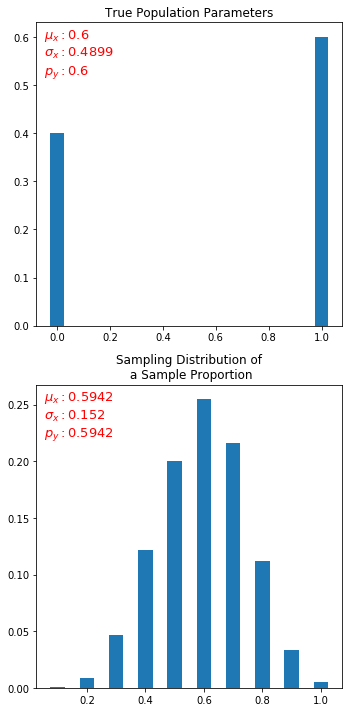
我想我已经解决了。通过逆向工程Rajesh的方法，并从Daniel暗示图形是否可能成为问题，最后我找出了罪魁祸首：默认条形图宽度为0.8太宽，无法显示我的图形在顶部变平。下面是修改后的代码和输出。

from SDSP import create_bernoulli_population, get_frequency_df
from random import shuffle, choices
from bi_to_nor_demo import get_metrics, bare_minimal_plot
import matplotlib.pyplot as plt

N = 10000  # 10000 balls
p = 0.6    # probability of yellow ball is 0.6, and others (1-0.6)=>0.4
n_pickups = 10       # sample size
n_experiments = 2000  # I dont know what this is called 


# THEORETICAL PDF
# generate population and calculate theoretical bernoulli pdf
population = create_bernoulli_population(N,p)
theor_df = get_frequency_df(population)


# STATISTICAL PDF
# choose sample, take mean and add to X_mean_list. Do this for n_experiments times. 
X_hat = []
X_mean_list = []
for each_experiment in range(n_experiments):
    X_hat = choices(population, k=n_pickups)  # choose, say 10 samples from population (with replacement)
    X_mean = sum(X_hat)/len(X_hat)
    X_mean_list.append(X_mean)
stats_df = get_frequency_df(X_mean_list)


# plot both theoretical and statistical outcomes
fig, (ax1,ax2) = plt.subplots(2,1, figsize=(5,10))
from SDSP import plot_pdf
mu,var,sigma = get_metrics(theor_df)
plot_pdf(theor_df, ax1, mu, sigma, p, title='True Population Parameters')
mu,var,sigma = get_metrics(stats_df)
plot_pdf(stats_df, ax2, mu, sigma, p=mu, bar_width=round(0.5/n_pickups,3),title='Sampling Distribution of\n a Sample Proportion')
plt.tight_layout()
plt.show()

输出：