多变量正常的Numpy向量化

Question

我有两个2D numpy数组A，B。我想使用scipy.stats.multivariate_normal来计算A中每行的联合logpdf，使用B中的每一行作为协方差矩阵。有没有一种方法可以在没有显式循环行的情况下执行此操作？将scipy.stats.multivariate_normal直接应用到A和B确实计算了A中每行的logpdf（这是我想要的），但是使用整个2D数组A作为协方差矩阵，这不是我想要的（我需要） B的每一行创建一个不同的协方差矩阵）。我正在寻找一个使用numpy矢量化的解决方案，并避免显式循环两个数组。

Answer 1

我也试图完成类似的事情。这是我的代码，它接收三个NxD矩阵。 X的每一行都是一个数据点，means的每一行都是一个平均向量，covariances的每一行都是对角协方差矩阵的对角矢量。结果是对数概率的长度为N的向量。

def vectorized_gaussian_logpdf(X, means, covariances):
    """
    Compute log N(x_i; mu_i, sigma_i) for each x_i, mu_i, sigma_i
    Args:
        X : shape (n, d)
            Data points
        means : shape (n, d)
            Mean vectors
        covariances : shape (n, d)
            Diagonal covariance matrices
    Returns:
        logpdfs : shape (n,)
            Log probabilities
    """
    _, d = X.shape
    constant = d * np.log(2 * np.pi)
    log_determinants = np.log(np.prod(covariances, axis=1))
    deviations = X - means
    inverses = 1 / covariances
    return -0.5 * (constant + log_determinants +
        np.sum(deviations * inverses * deviations, axis=1))

请注意，此代码仅适用于对角协方差矩阵。在这种特殊情况下，下面的数学定义被简化：行列式成为元素的乘积，逆变为元素的倒数，矩阵乘法变为逐元乘法。

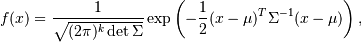
快速测试正确性和运行时间：

def test_vectorized_gaussian_logpdf():
    n = 128**2
    d = 64

    means = np.random.uniform(-1, 1, (n, d))
    covariances = np.random.uniform(0, 2, (n, d))
    X = np.random.uniform(-1, 1, (n, d))

    refs = []

    ref_start = time.time()
    for x, mean, covariance in zip(X, means, covariances):
        refs.append(scipy.stats.multivariate_normal.logpdf(x, mean, covariance))
    ref_time = time.time() - ref_start

    fast_start = time.time()
    results = vectorized_gaussian_logpdf(X, means, covariances)
    fast_time = time.time() - fast_start

    print("Reference time:", ref_time)
    print("Vectorized time:", fast_time)
    print("Speedup:", ref_time / fast_time)

    assert np.allclose(results, refs)

我获得了大约250倍的加速。 （是的，我的申请要求我计算16384个不同的高斯人。）