这个函数的时间复杂度是O(1)吗?
我今天正在审查有关算法的一些旧笔记,这让我想到了。
复杂性
O(1)表示函数的执行时间与数据无关。
因此,假设我们有一个函数来添加数组中的所有元素。
int add(int[] array){
int sum =0;
for (int i=0;i<ARRAY_MAX_SIZE;i++){
sum= sum + (i<array.length?array[i]:0);
}
return sum;
}
其中ARRAY_MAX_SIZE是数组的最大可能大小。我知道这段代码效率不高,我不想讨论这个问题。但是,运算符+每次都被称为相同的金额时间,并且不受数据大小的影响。
这是否意味着此功能的复杂性为O(1)?
4 个答案:
答案 0 :(得分:6)
是。 O(1)表示恒定时间,而不是快速/有效/最佳。
Big-O复杂性忽略了常量步骤的复杂性。分裂(慢)就像&#34;复杂&#34;作为增量(快)。
答案 1 :(得分:4)
实际答案是“它取决于”。
这里发生了两组不同的事情:
-
ARRAY_MAX_SIZE次,你:- 递增并测试for循环
- 添加到总数
-
array.length次,你:;- 访问
array[i]
- 访问
-
ARRAY_MAX_SIZE - array.length次,你:;- 加载常数零
所以总运行时间是
t = k_1 * ARRAY_MAX_SIZE +
k_2 * n +
k_3 * (ARRAY_MAX_SIZE - n)
所以你看看k_2和k_3的比较方式。它们基本相同吗?然后它是O(1)。是k_2 >> k_3吗?然后它是O(n)。
为什么k_2 >> k_3?因为array[i]正在访问内存,memory is comparatively very slow:
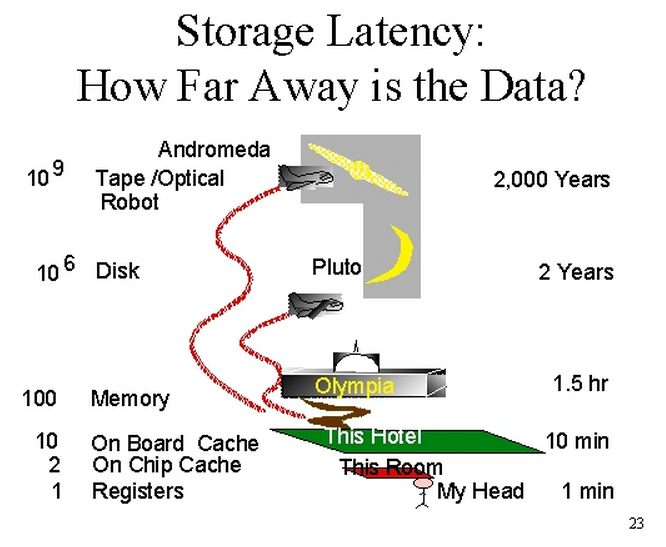
答案 2 :(得分:2)
唯一有趣的部分是array[i]仅使用n次。这意味着您添加一个操作来对数组进行处理,以使i元素仅n次。我不会这么算,但是这不可能成为O(n)吗?只是扮演魔鬼的拥护者。
我认为这将是真正的O(1)等价物。
int add(int[] array){
int sum =0;
int len = array.length;
for (int i=0;i<ARRAY_MAX_SIZE;i++){
sum= sum + array[i%len] & (i < len ? 0xFFFFFFFF : 0);
}
return sum;
}
答案 3 :(得分:-1)
如果你有一个最大的数组大小,那么复杂性将是O(1)。但这还有其他后果。 array.length需要小于ARRAY_MAX_SIZE,,因此array.length以常数为界,同时生成以下O(1):
for(int i=0; i<array.length; i++) {
sum = sum + array[i];
}
因此,我们通常会忽略对数组大小的任何限制,以便为算法的复杂性获得有用的结果。
这显然假设ARRAY_MAX_SIZE是数组的最大可能大小(正如问题中定义的那样),而不是其他值。
相关问题
最新问题
- 我写了这段代码,但我无法理解我的错误
- 我无法从一个代码实例的列表中删除 None 值,但我可以在另一个实例中。为什么它适用于一个细分市场而不适用于另一个细分市场?
- 是否有可能使 loadstring 不可能等于打印?卢阿
- java中的random.expovariate()
- Appscript 通过会议在 Google 日历中发送电子邮件和创建活动
- 为什么我的 Onclick 箭头功能在 React 中不起作用?
- 在此代码中是否有使用“this”的替代方法?
- 在 SQL Server 和 PostgreSQL 上查询,我如何从第一个表获得第二个表的可视化
- 每千个数字得到
- 更新了城市边界 KML 文件的来源?