Question

我一直在学习Ruby，所以我想我会尝试一些项目的Euler难题。令人尴尬的是，我只是解决了问题4 ...

问题4如下：

回文编号读取相同的内容   双向。最大的回文制作   从两个2位数的产品   数字是9009 = 91×99。
     找到最大的回文组织   两个3位数的乘积。

所以我想我会在一个嵌套的for循环中从999循环到100并对回文进行测试，然后当我找到第一个（应该是最大的一个）时突破循环：

final=nil
range = 100...1000
for a in range.to_a.reverse do
  for b in range.to_a.reverse do
    c=a*b
    final=c if c.to_s == c.to_s.reverse
    break if !final.nil?
  end
  break if !final.nil?
end
puts final

这确实输出了回文580085，但显然这不是该范围内两个三位数字的最高乘积。奇怪的是，如果我将范围更改为10 ... 100，则相同的代码成功返回9009，就像在示例中一样。

有人可以告诉我我要去哪里错？
此外，有没有更好的方法打破内部循环？

由于

Answer 1

您正在测试999 *（999 ... 100），然后是998 *（999 ... 100）

因此，在测试997 * 996之前，您将测试999 * 500。

那么，我们如何找到合适的号码？

首先注意乘法是反射的，a * b == b * a，所以b每次都不需要从999 ... 0开始，只需要... 0。

当你找到一个palindrone时，将两个因素加在一起并保存总和（同时保存这两个因素）

在循环内部，如果（a + b）小于保存的总和，则放弃内循环并移动到下一个a。当a低于sum / 2时，你找不到的未来值将高于你已经找到的值，所以你已经完成了。

Answer 2

问题是你可能会找到a为999且b为200的回文，但是你太早了，所以你永远不会看到998 * 997（只是示例数字）。

您需要查找所有回文，或者在找到第一个回文后，将b设置为最小界限并继续浏览a循环。

Answer 3

关于第二个问题，我的建议是以更具功能性而非程序性的方式处理问题。因此，您可以尝试在功能上“描述”您的问题，而不是循环，让Ruby完成工作：

从所有3位数字对中，
- select只有那些产品是回文的人，
  - 找到产品最多的

虽然这种方法可能无法提供最有效的解决方案，但它可能会教你几个Ruby习语。

Answer 4

考虑P的数字 - 让它们为x，y和z。 P必须至少为6位数，因为回文111111 = 143×777 - 两个3位整数的乘积。由于P是回文：

P=100000x + 10000y + 1000z + 100z + 10y + x
P=100001x + 10010y + 1100z
P=11(9091x + 910y + 100z)

由于11是素数，所以整数a或b中的至少一个必须具有11的因子。因此，如果a不能被11整除，那么我们知道b必须是。使用此信息，我们可以根据a。

确定我们检查的b值

Answer 5

C＃实施：

using System;

namespace HighestPalindrome
{
    class Program
    {
        static void Main(string[] args)
        {
            int i, j;
            int m = 1;
            bool flag = false;

            while (true)
            {
                if (flag) j = m + 1;
                else j = m;

                for (i = m; i > 0; i--)
                {
                    Console.WriteLine("{0} * {1} = {2}", 1000 - i, 1000 - j, (1000 - i) * (1000 - j));
                    j++;

                    //--- Palindrome Check ------------------------------

                    int number, temp, remainder, sum = 0;
                    number = temp = (1000 - i) * (1000 - j);

                    while (number > 0)
                    {
                        remainder = number % 10;
                        number /= 10;
                        sum = sum * 10 + remainder;
                    }

                    if (sum == temp)
                    {
                        Console.WriteLine("Highest Palindrome Number is - {0} * {1} = {2}", 1000 - i, 1000 - j, temp);
                        Console.ReadKey();
                        return;
                    }

                    //---------------------------------------------------
                }

                if (flag)
                    m++;
                flag = !flag;
            }

        }
    }
}

Answer 6

错误在于你假设如果你发现最大值为a的palindrom，它会给出最好的产品，这是不正确的。解决方案是保留max_product值并根据您找到的解决方案进行更新。

Answer 7

我可以回答你的第一个问题：你需要找到最高的产品，而不是含有最高因子的产品。换句话说，即使a * b，c * d也可能大于c > a > b。

Answer 8

你在第一个回归的时候打破了，不一定是最大的。

假设您有A，B，C，D，E。在测试D * C之前测试E * A.

Answer 9

ar=[]
limit = 100..999
for a in limit.to_a.reverse do
  for b in (100..a).to_a.reverse do
    c=a*b
    if c.to_s == c.to_s.reverse
      palndrm=c 
      ar << palndrm
    end  
  end
end
print ar
print"\n"
puts ar.max
puts ar.min

Answer 10

实施：

max = 100.upto(999).inject([-1,0,0]) do |m, a|
  a.upto(999) do |b|
    prod = a * b
    m = [prod, a, b] if prod.to_s == prod.to_s.reverse and prod > m[0]
  end
  m
end
puts "%d = %d * %d" % max

打印906609 = 913 * 993

Answer 11

主要是要经历所有可能的价值观。当你发现第一个答案只是以零的最佳答案开始然后尝试所有组合并保持最佳更新时，不要试图打破。次要的是尝试减少“所有组合”的集合。

您可以做的一件事是将内循环限制为小于或等于a的值（因为 b == b a）。这使得等式中较大的值总是在a中，并且大大减少了必须测试的值的数量。

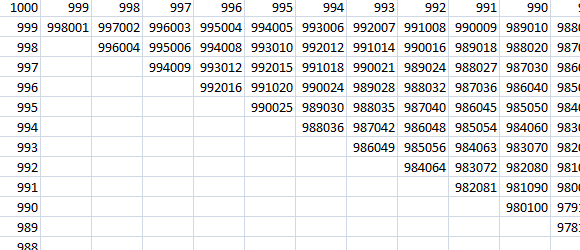
alt text

for a in range.to_a.reverse do
    for b in (100..a).to_a.reverse do

当产品低于当前最佳值时，您可以做的下一件事是打破内循环。

c = a*b
next if c < best

接下来，如果你打算全部通过它们，反过来通过它们是没有好处的。通过从范围的顶部开始，在找到回文数字之前需要一段时间，因此需要一段时间来减少搜索集。如果从底部开始，则开始快速增加下限。

for a in range.to_a do
    for b in (100..a).to_a do

我的测试显示无论哪种方式你尝试了一些405K对。那么如何以不同的方式思考问题呢。两个3位数字的最大可能产品是多少？ 999 * 999 = 998001，最小的是100 * 100 = 10000.我们如何看待您在第一个答案上打破的想法，但将其应用于不同的范围，即998001到10000（或999 * 999到100 *） 100）。

for c in (10000...998001).to_a.reverse do

我们在经过202次测试后才进入回文......问题是它不是两个3位数字的乘积。所以现在我们必须检查我们发现的回文是否是2个3位数字的乘积。一旦我们找到了回文范围内的值和两个3位数字的乘积，我们就完成了。我的测试显示我们发现在不到93K的测试后，满足要求的最高回文。但是，由于我们要检查所有回文都是两个3位数字的产品，所以它可能没有比以前的解决方案更有效。

让我们回到最初的改进。

for a in range.to_a.reverse do
    for b in (100..a).to_a.reverse do

我们循环行然后是列并尝试通过检测我们可以转到下一行的点来提高效率，因为当前行上的任何其他trys可能不会比我们当前最好的更好。如果我们穿过对角线而不是走下去，会怎么样？

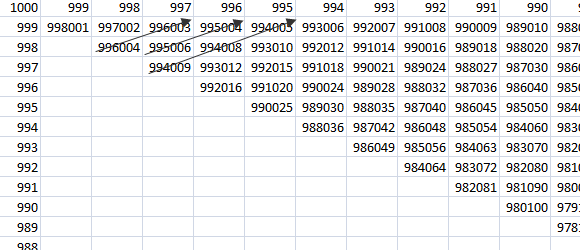
alt text

由于产品从对角线逐渐变小，因此只要找到了一个回文数字就可以停止。这是一个非常有效的解决方案，但实现起来更复杂。事实证明，这种方法在略超过2200 trys之后找到了最高的回文数。

Answer 12

这是我在Ruby中提出的：

def largest_palindrome_product(digits)
  largest, upper, lower = 0, 10**digits - 1, 10**(digits - 1)

  for i in upper.downto(lower) do
    for j in i.downto(lower) do
      product = i * j
      largest = product if product > largest && palindrome?(product)
    end
  end
  largest
end

这是检查数字是否为回文的功能：

def palindrome?(input)
  chars = input.to_s.chars
  for i in 0..(chars.size - 1) do
    return false if chars[i] != chars[chars.size - i - 1]
  end
  true
end

我想那里可能有一个更有效的解决方案。

Answer 13

对于这个问题，因为我们正在寻找最高的palindrom，我认为它将从9开始。因此以9（palindrom）结束。

如果你注意，要获得9的数字，你只能得到9和1,3和3,7和7的数字。

然后检查其他值是没用的（例如999 * 998，因为它不会以9结尾）。

从999和991开始，你可以减去10到991，尝试999和981等... 您也可以使用993和993 ... 993 * 983 与997 * 997相同，然后是997 * 987等您不需要超过900或10 ^ 4 - 10 ^ 3，因为您可以确定之前的最高值。

int PB4_firstTry(int size)
{
    int nb1 = (int)pow(10.0,size+1.0) - 1, nb2 = (int)pow(10.0,size+1.0) - 1;
    int pal91 = getFirstPalindrome(size,9,1);
    int pal33 = getFirstPalindrome(size,3,3);
    int pal77 = getFirstPalindrome(size,7,7);

    int bigger1 = (pal91 > pal33) ? pal91 : pal33;
    return (bigger1 > pal77) ? bigger1 : pal77;
}

int getFirstPalindrome(int size,int ending1,int ending2)
{
    int st1 =  (int)pow(10.0,size+1.0) - 10 + ending1;
    int comp = st1 - pow(10.0,size);
    int st2 =  (int)pow(10.0,size+1.0) - 10 + ending2;
    int answer = -1;
    while (st1 > comp)
    {
        for (int i = st2; i > comp && st1*i > answer; i-=10)
        {
            if (PB4_isPalindrome(st1*i))
                answer = st1*i;
        }
        st1 -= 10;
    }
    return answer;
}

bool PB4_isPalindrome(int number)
{
    std::string str = intToString(number);
    for (int i = 0; i < (int)(str.length() / 2); i++)
    {
        if (str[i] != str[str.length() - 1 - i])
            return false;
    }
    return true;
}

std::string intToString(int number)
{
    std::ostringstream convert;
    convert << number;
    return convert.str();
}

当然，这适用于4个大小的数字因子等。

对于回文产品问题感到困惑

13 个答案: