Question

我被要求编写一个递归函数，用于计算沿着网格边缘的单调格子路径的加泰罗尼亚数，其中n×n个方格单元格不会越过对角线（pic）<登记/>
我不被允许使用for循环，只允许递归调用......这就是我所做的：

public long C(int n) {
    if (n == 1)
        return 0;
    return C(n, 0, 0);
}

private long C(int n, int i, int j) {

    // CAN MOVE UP & RIGHT
    if (j - i > 0 && j + 1 <= n)
        return paths(n, i + 1, j) + paths(n, i, j + 1);
    // CAN MOVE UP
    else if (j - i > 0)
        return paths(n, i + 1, j);
    // CAN MOVE RIGHT
    else if (j + 1 <= n)
        return paths(n, i, j + 1);
    // CAN'T MOVE
    else
        return 1;
}

我不知道这段代码是否最好但是它有效...我想将此函数转换为Memoized函数。但我无法理解＆amp;也为什么它会使功能更有效。我理解为什么备忘录中的Fibonnaci效率更高，但在这里我总是必须到达路径的末尾，然后返回1或0，那么如果我将1/0存储在数组中，那么重要的是什么？

感谢您提供任何帮助

Answer 1

但我无法理解为什么它会使功能更有效。

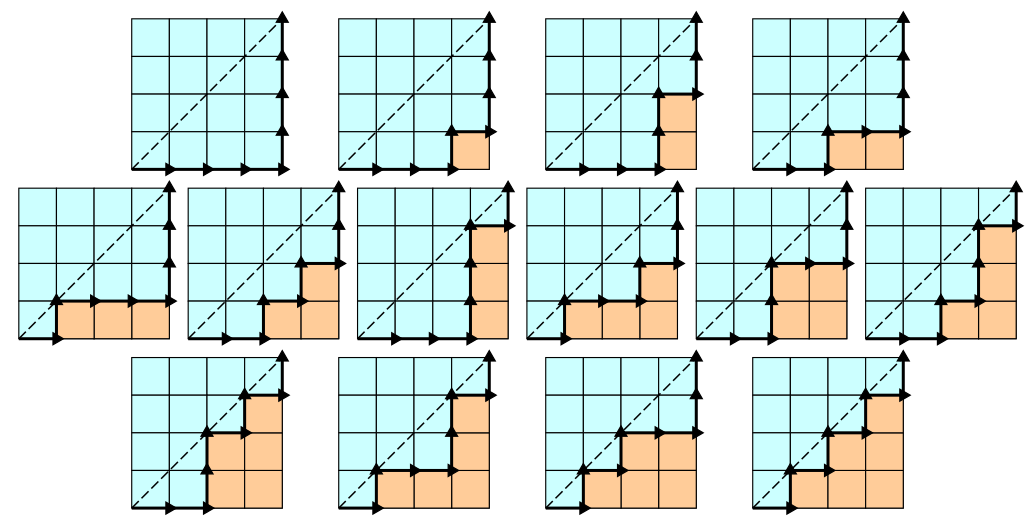
查看图像，以1开头编号的图片，左下角的(x,y)坐标(0,0)，你可以看到图片2,3,4,5,6,7， 8,10,12都在(3,1)处进行。

来自(3,1)的路径：

(3,1) → (4,1) ↑ (4,2) ↑ (4,3) ↑ (4,4)
- 图片2,4,5
(3,1) ↑ (3,2) → (4,2) ↑ (4,3) ↑ (4,4)
- 图片3,6,8
(3,1) ↑ (3,2) ↑ (3,3) → (4,3) ↑ (4,4)
- 图片7,10,12

如您所见，您走了相同的路径多次（3）次。如果您可以缓存（memoize）从(3,1)到结尾有3条路径的事实，那么您可以节省时间。

随着电网变大，节省的时间将会增加。

所以，你所做的，就是你第一次达到某一点，就像你已经做的那样用递归计算结果，然后保存那个点的数字，当你再次达到这一点时，你只需要使用缓存的值：

public static long paths(int n) {
    if (n == 1)
        return 0;
    return paths(n, 0, 0, new long[n][n]);
}
private static long paths(int n, int y, int x, long[][] cache) {
    long result = cache[y][x];
    if (result == 0) {
        if (y < x && x < n) // CAN MOVE UP & RIGHT
            result = paths(n, y + 1, x, cache) + paths(n, y, x + 1, cache);
        else if (y < x) // CAN MOVE UP
            result = paths(n, y + 1, x, cache);
        else if (x < n) // CAN MOVE RIGHT
            result = paths(n, y, x + 1, cache);
        else // CAN'T MOVE
            result = 1;
        cache[y][x] = result;
    }
    return result;
}

Answer 2

您似乎知道Memoization是什么。基本上，您所做的只是创建一个表memo，一旦您到达它就存储一个值，这样您就不必再次在递归中计算它。类似于fibonacci(5)为什么不必进入递归以查找fibonacci(3)的内容，如果我们已经计算过，请说fibonacci(6)，因为我们已经记住了它。我希望你明白。这是代码，以同样的精神记忆。安德里亚的问题有很好的视觉效果可供理解。

long[][]memo;  //Memo table

public long C(int n)
{
    if (n == 1)
        return 0;

    memo=new int[n+1][n+1]; //Increase to n+1 and won't crash!

    for(int i=0;i<=n;i++)
        for(int j=0;j<=n;j++)
            memo[j][i]=-1;

    return C(n, 0, 0, memo);
}

private long C(int n, int i, int j, it) {

    // CAN MOVE UP & RIGHT
    if (j - i > 0 && j + 1 <= n)
    {
        if(memo[i+1][j]==-1)
            memo[i+1][j]=paths(n, i + 1, j);

        if(memo[i][j+1]==-1)
            memo[i][j+1]=paths(n, i, j + 1);

        return memo[i+1][j]+memo[i][j+1];
    }
    // CAN MOVE UP
    else if (j - i > 0)
    {
        if(memo[i+1][j]==-1)
            memo[i+1][j]=paths(n, i + 1, j);
        return memo[i+1][j];
    }
    // CAN MOVE RIGHT
    else if (j + 1 <= n)
    {
        if(memo[i][j+1]==-1)
            memo[i][j+1]=paths(n, i, j + 1);
        return memo[i][j+1];
    }
    // CAN'T MOVE
    else
        return 1;
}

将加泰罗尼亚语数递归到Memoized

2 个答案: