Question

我试图实现这一点但没有成功，我必须这样做而不使用外部模块numpy等。应用程序中有3个模块我正在编写这个，Python和C＃，C ++但除了标准之外没有其他花哨的库的。

在另一个应用程序中，我使用了numpy的svd，它的工作原理非常准确。所以我用它来匹配我的结果。我的方法是PCA，到目前为止一切都很好。但在我计算出对称协方差矩阵后，我不知道如何找到最大的特征向量。

数据集总是3d点，x，y和z。

vector center;
for(point p in points):
    center += p;
center /= points.count;

sumxx = 0;
sumxy = 0;
sumxz = 0;
sumyy = 0;
sumyz = 0;
sumzz = 0;
for(point p in points):
    vector s = p - center;
    sumxx += s.x * s.x;
    sumxy += s.x * s.y;
    sumxz += s.x * s.z;
    sumyy += s.y * s.y;
    sumyz += s.y * s.z;
    sumzz += s.z * s.z;

matrix3 mat = invert(matrix3(sumxx, sumxy, sumxz, sumxy, sumyy, sumyz, sumxz, sumyz, sumzz));
vector n;
if (determinant(mat) > 0)
    normal = find_largest_eigenvalue

Answer 1

让我们回顾一下你的要求，澄清一下：

找到矩阵mat
此特征向量应与矩阵的最大特征值相关联
矩阵是principal component analysis的对称协方差矩阵。 特别是它是对称的。
您的矩阵是正方形，大小为3 x 3 ，如您的代码matrix3 mat = ...所示，并在（现已删除）评论中得到确认。

在这些非常具体的情况下，以下答案适用。然而，tmyklebu警告这种方法对某些病理矩阵的数值不稳定性，通常在r接近-1时。

好的，让我们先从wikipedia's page on Characteristic polynomials

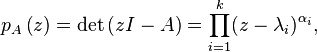
在线性代数中，方阵的特征多项式是多项式，它在矩阵相似下是不变的，并且具有特征值作为根。 $det(zI-A)$

3x3 matrix section in the page on Eigenvalue algorithms

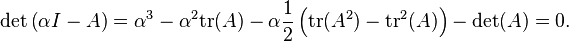
如果A是3×3矩阵，则其特征方程可表示为： $det(zI-A)$

后面几行（或多或少）这个伪代码，用于对称矩阵（你说你有，如果我没有弄错 - 否则你可能有复杂的特征值）：

p1 = A(1,2)^2 + A(1,3)^2 + A(2,3)^2
if (p1 == 0) 
   % A is diagonal.
   eig1 = A(1,1)
   eig2 = A(2,2)
   eig3 = A(3,3)
else
   q = (A(1,1) + A(2,2) + A(3,3)) / 3
   p2 = (A(1,1) - q)^2 + (A(2,2) - q)^2 + (A(3,3) - q)^2 + 2 * p1
   p = sqrt(p2 / 6)
   B = (1 / p) * (A - q * I)       % I is the identity matrix
   r = determinant(B) / 2

   % In exact arithmetic for a symmetric matrix  -1 <= r <= 1
   % but computation error can leave it slightly outside this range.
   if (r <= -1) 
      phi = pi / 3
   elseif (r >= 1)
      phi = 0
   else
      phi = acos(r) / 3
   end

   % the eigenvalues satisfy eig3 <= eig2 <= eig1
   eig1 = q + 2 * p * cos(phi)
   eig3 = q + 2 * p * cos(phi + (2*pi/3))
   eig2 = 3 * q - eig1 - eig3     % since trace(A) = eig1 + eig2 + eig3
end

所以你想在第一种情况下max(eig1,eig2,eig3)，在第二种情况下需要eig1。让我们称e这个最大的特征值。

对于特征向量，您现在可以解决(A-e*I)x=0

Answer 2

有不同的算法可以找到特征值。有些工作从最小到最大，如QR;其他工作从最大到最小，如电源迭代或Jacobi-Davidson。

也许你想要的算法切换。尝试电源方法，看看是否有帮助。

https://scicomp.stackexchange.com/questions/1681/what-is-the-fastest-way-to-calculate-the-largest-eigenvalue-of-a-general-matrix

如何找到矩阵的最大特征向量？

2 个答案: