使用任意精度数学的log（）算法示例

Question

我正在寻找一种可以在PHP中实现的算法，以使用任意精度数学获得整数的自然log（）。我受限于GMP库的PHP覆盖库（有关PHP中可用的GMP函数，请参阅http://php.net/manual/en/ref.gmp.php。）

如果您知道可以转换为PHP的通用算法，那么这也是一个有用的起点。

PHP支持本机log（）函数，我知道，但我希望能够使用任意精度来解决这个问题。

密切相关的是获取exp（）函数。如果我的男生Maths对我有用，那么获得一个可以导致另一个。

Answer 1

那么你会有泰勒系列，可以重写以获得更好的收敛

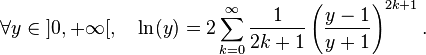
要将这个好的等式转换为算法，您必须了解聚合序列如何工作：每个术语越来越小。这种减少发生得足够快，因此总和是一个有限值：ln（y）。

由于实数的好属性，你可以认为序列收敛到ln（y）：

• L（1）= 2/1 *（y-1）/（y + 1）
• L（2）= 2/1 *（y-1）/（y + 1）+ 2/3 *（（y-1）/（y + 1））^ 3
• L（3）= 2/1 *（y-1）/（y + 1）+ 2/3 *（（y-1）/（y + 1））^ 3 + 2/5 *（（ y-1）/（y + 1））^ 5

..等等。

显然，计算这个序列的算法很简单：

x = (y-1)/(y+1);
z = x * x;
L = 0;
k = 0;
for(k=1; x > epsilon; k+=2)
{
    L += 2 * x / k;
    x *= z;
}

在某些时候，你的x会变得很小，以至于它不再有助于L的有趣数字，而只是修改小得多的数字。如果这些修改对您的目的而言过于微不足道，您可能会停止。

因此，如果你想达到1e ^ -20的精度，那么将epsilon设置得比那个小得多，你就可以了。

---

如果可以的话，不要忘记在日志中进行分解。如果它是一个完美的正方形，例如，ln（a²）= 2 ln（a） 实际上，当（y-1）/（y + 1）较小时，系列会收敛得更快，因此当y更小（或者更接近1时，如果你计划使用整数，那么它应该是等价的）。