如何在MATLAB中确定线性回归线的系数？

Question

我要编写一个程序，其中输入是2D点的数据集，输出是最小拟合线的回归系数，通过最小化最小MSE误差。

我想要处理一些示例点：

  X      Y
1.00    1.00
2.00    2.00
3.00    1.30
4.00    3.75
5.00    2.25

我将如何在MATLAB中执行此操作？

具体来说，我需要得到以下公式：

y = A + Bx + e

A是截距，B是斜率，而e是每点的残差。

Answer 1

根据您提供的链接以及我对您的问题的理解，您需要计算一组数据点的最佳拟合线。您还希望从第一原则开始。这将需要一些基本的微积分以及一些线性代数来求解2 x 2方程组。如果你回忆一下线性回归理论，我们希望找到最佳斜率m和截距b，以便对一组点([x_1,y_1], [x_2,y_2], ..., [x_n,y_n])（即我们n数据点），我们希望最小化此行与数据点之间的残差平方和。

换句话说，我们希望最小化成本函数F(m,b,x,y)：

m和b是此最佳拟合线的斜率和截距，而x和y是 x <的向量/ strong>和 y 构成数据集的坐标。

此函数是凸的，因此我们可以确定最小的最小值。可以通过查找关于每个参数的导数并将它们设置为等于0来确定最小值。然后我们求解m和b。这背后的直觉是我们同时找到m和b，以便通过这两个参数联合最小化成本函数。换句话说：

好的，让我们找到第一个数量：

我们可以从导数中减去因子2，因为等式的另一边等于0，我们也可以通过乘以-x_i项来进行一些术语分布：

接下来，让我们解决下一个参数：

我们可以再次降低因子2并在整个表达式中分配-1：

知道只是n，我们可以将上述内容简化为：

现在，我们需要使用上述两个等式同时求解m和b。这将共同最小化成本函数，该函数为我们的数据点找到最佳拟合线。

做一些重新安排，我们可以在方程式的一侧隔离m和b，而在另一侧隔离其余部分：

如您所见，我们可以将其表示为2 x 2方程组，以求解m和b。具体来说，让我们重新排列上面的两个方程式，使其呈矩阵形式：

---

关于上述问题，我们可以通过求解线性系统来分解问题：Ax = b。您所要做的就是解决x，x = A^{-1}*b。为了找到2 x 2系统的逆，给定矩阵：

反过来就是：

因此，通过将我们的数量代入上面的等式，我们以矩阵形式求解m和b，并简化为：

执行此乘法并分别求解m和b，这样可以得出：

因此，要找到最佳坡度和截距以最适合您的数据，您需要使用上述公式计算m和b。

鉴于您在评论中的链接中指定了您的数据，我们可以非常轻松地完成此任务：

%// Define points
X = 1:5;
Y = [1 2 1.3 3.75 2.25];

%// Get total number of points
n = numel(X);

% // Define relevant quantities for finding quantities
sumxi = sum(X);
sumyi = sum(Y);
sumxiyi = sum(X.*Y);
sumxi2 = sum(X.^2);
sumyi2 = sum(Y.^2);

%// Determine slope and intercept
m = (sumxi * sumyi - n*sumxiyi) / (sumxi^2 - n*sumxi2);
b = (sumxiyi * sumxi - sumyi * sumxi2) / (sumxi^2 - n*sumxi2);

%// Display them
disp([m b])

......我们得到：

0.4250  0.7850

因此，最小化误差的最佳拟合线是：

y = 0.4250*x + 0.7850

---

但是，如果您想使用内置的MATLAB工具，可以使用polyfit（信用转到Luis Mendo提供提示）。 polyfit通过最小化最佳拟合线与数据点之间的平方误差之和来确定线性回归的最佳拟合线（或n ^th 次多项式曲线而非......）。你如何调用这个函数是这样的：

coeff = polyfit(x,y,order);

x和y是数据的x和y点，而order确定您想要的最佳拟合线的顺序。例如，order=1表示该行是线性的，order=2表示该行是二次的，依此类推。基本上，polyfit适合给定数据点的order多项式。鉴于您的问题，order=1。因此，根据链接中的数据，您只需执行以下操作：

X = 1:5;
Y = [1 2 1.3 3.75 2.25];
coeff = polyfit(X,Y,1)

coeff =

    0.4250    0.7850

coeff的工作方式是这些是回归线的系数，从递减值的最高阶开始。因此，上述coeff变量意味着回归线拟合为：

y = 0.4250*x + 0.7850

第一个系数是斜率，而第二个系数是截距。您还会看到这与您提供的链接相符。

如果你想要一个直观的表示，这里有一个数据点的图表以及最符合这些要点的回归线：

plot(X, Y, 'r.', X, polyval(coeff, X));

这是情节：

polyval采用一系列系数（通常由polyfit生成），并提供一组x坐标，并计算y值是什么给定x的值。从本质上讲，您正在评估最佳拟合线上的点。

---

编辑 - 扩展到更高的订单

如果你想扩展以便找到最适合任何n ^th 阶多项式的东西，我不会详细说明，但它归结为构造以下线性系统。给出(x_i, y_i)：

之间i ^th 点的关系

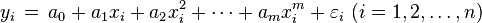
您将构建以下线性系统：

基本上，您可以创建一个点y的矢量，然后构建一个矩阵X，使每列显示您的点矢量x并应用幂运算每一栏。具体地，第一列是第零功率，第一列是第一功率，第二列是第二功率，依此类推。你会这样做直到m，这是你想要的阶多项式。 e的向量将是集合中每个点的残差。

具体而言，问题的表述可以用矩阵形式写成：

构建此矩阵后，您可以通过计算pseudo-inverse找到最小二乘法的参数。如何导出伪逆，你可以在我链接的维基百科文章中读到它，但这是通过最小二乘法最小化系统的基础。伪逆是最小二乘最小化的支柱。具体做法是：

(X^{T}*X)^{-1}*X^{T}是伪逆。 X本身是一个非常流行的矩阵，称为Vandermonde matrix，MATLAB有一个名为vander的命令来帮助您计算该矩阵。一个小小的注释是MATLAB中的vander以相反的顺序返回。权力从m-1减少到0.如果您想要反转，您需要在该输出矩阵上调用fliplr。此外，您还需要在其末尾追加一列，即将所有元素提升到m ^th 幂的向量。

我不知道你如何重复你的例子以获得比线性更高的顺序。我将此作为学习练习留给您，但只需构建向量y，矩阵X和vander，然后通过应用伪 - 找到参数与上述X相反以解决您的参数。

---

祝你好运！