C中精度浮点运算的问题

Question

对于我的一个课程项目，我开始在C中实现“朴素贝叶斯分类器”。我的项目是使用大量的训练数据实现文档分类器应用程序（尤其是垃圾邮件）。

由于C数据类型的限制，现在我在实现算法时遇到了问题。

（我在这里使用的算法，http://en.wikipedia.org/wiki/Bayesian_spam_filtering）

问题陈述： 该算法涉及获取文档中的每个单词并计算它是垃圾词的概率。如果p1，p2 p3 .... pn是字-1,2,3 ... n的概率。使用

计算doc是否为垃圾邮件的概率

这里，概率值可以非常容易地在0.01左右。因此，即使我使用数据类型“double”，我的计算也会进行折腾。为了证实这一点，我写了一个下面给出的示例代码。

#define PROBABILITY_OF_UNLIKELY_SPAM_WORD     (0.01)
#define PROBABILITY_OF_MOSTLY_SPAM_WORD     (0.99)

int main()
{
    int index;
    long double numerator = 1.0;
    long double denom1 = 1.0, denom2 = 1.0;
    long double doc_spam_prob;

    /* Simulating FEW unlikely spam words  */
    for(index = 0; index < 162; index++)
    {
        numerator = numerator*(long double)PROBABILITY_OF_UNLIKELY_SPAM_WORD;
        denom2    = denom2*(long double)PROBABILITY_OF_UNLIKELY_SPAM_WORD;
        denom1    = denom1*(long double)(1 - PROBABILITY_OF_UNLIKELY_SPAM_WORD);
    }
    /* Simulating lot of mostly definite spam words  */
    for (index = 0; index < 1000; index++)
    {
        numerator = numerator*(long double)PROBABILITY_OF_MOSTLY_SPAM_WORD;
        denom2    = denom2*(long double)PROBABILITY_OF_MOSTLY_SPAM_WORD;
        denom1    = denom1*(long double)(1- PROBABILITY_OF_MOSTLY_SPAM_WORD);
    }
    doc_spam_prob= (numerator/(denom1+denom2));
    return 0;
}

我尝试了Float，double甚至是long double数据类型，但仍然存在同样的问题。

因此，在我正在分析的一个100K字的文件中，如果只有162个单词的垃圾邮件概率为1％，剩余的99838个是明显的垃圾邮件单词，那么我的应用程序仍会因为精度错误而将其称为非垃圾邮件doc（如分子很容易转到ZERO !!!!

这是我第一次遇到这样的问题。那么究竟应该如何解决这个问题呢？

Answer 1

这通常发生在机器学习中。 AFAIK，关于精度的损失你无能为力。因此，为了绕过这一点，我们使用log函数并将除法和乘法转换为减法和加法，分别为

。

所以我决定做数学，

原始等式是：

我稍微修改一下：

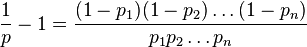
双面记录日志：

让，

代，

因此，计算组合概率的替代公式：

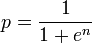
如果您需要我对此进行扩展，请发表评论。

Answer 2

这是一个技巧：

for the sake of readability, let S := p_1 * ... * p_n and H := (1-p_1) * ... * (1-p_n), 
then we have:

  p = S / (S + H)
  p = 1 / ((S + H) / S)
  p = 1 / (1 + H / S)

let`s expand again:

  p = 1 / (1 +  ((1-p_1) * ... * (1-p_n)) / (p_1 * ... * p_n))
  p = 1 / (1 + (1-p_1)/p_1 * ... * (1-p_n)/p_n)

基本上，您将获得一个数字相当大的产品（0和p_i = 0.01之间，99）。我们的想法是，不要将大量的小数字彼此相乘，以获得0，而是为了得到两个小数的商。例如，如果n = 1000000 and p_i = 0.5 for all i，则上述方法会为您0/(0+0)提供NaN，而建议的方法会为您提供1/(1+1*...1)，即0.5。

当所有p_i被排序并且你以相反的顺序对它们进行配对时（假设为p_1 < ... < p_n），你可以获得更好的结果，那么下面的公式将获得更好的精度：

  p = 1 / (1 + (1-p_1)/p_n * ... * (1-p_n)/p_1)

这样你就可以将大分子（小p_i）与大分母（大p_(n+1-i)）以及小分子与小分母分开。

编辑：MSalter在他的回答中提出了一个有用的进一步优化。使用它，公式如下：

  p = 1 / (1 + (1-p_1)/p_n * (1-p_2)/p_(n-1) * ... * (1-p_(n-1))/p_2 * (1-p_n)/p_1)

Answer 3

您的问题是由于您收集太多条款而不考虑其大小而引起的。一种解决方案是采用对数。另一个是对您的个人条款进行排序。首先，让我们将等式重写为1/p = 1 + ∏((1-p_i)/p_i)。现在你的问题是某些术语很小，而其他术语很大。如果你连续有太多的小术语，你会下流，而且有太多大术语你会溢出中间结果。

所以，不要连续放多少相同的订单。对术语(1-p_i)/p_i进行排序。结果，第一个是最小的，最后一个是最大的。现在，如果你马上将它们相乘，你仍然会有下溢。但计算顺序无关紧要。在临时集合中使用两个迭代器。一个从头开始（即(1-p_0)/p_0），另一个在结尾（即(1-p_n)/p_n），你的中间结果从1.0开始。现在，当你的中间结果是> = 1.0时，你从前面拿一个术语，当你的中间结果是＆lt; 1.0你从后面得到一个结果。

结果是，当您使用术语时，中间结果将在1.0附近振荡。当你用完小或大的时候，它只会上升或下降。但那没关系。那时，你已经消耗了两端的极值，因此中间结果将慢慢接近最终结果。

当然有溢出的可能性。如果输入完全不可能是垃圾邮件（p = 1E-1000），则1/p将溢出，因为∏((1-p_i)/p_i)溢出。但由于术语已排序，我们知道如果∏((1-p_i)/p_i)溢出，中间结果将仅溢出 。因此，如果中间结果溢出，则不会出现后续的精度损失。

Answer 4

尝试计算逆1 / p。这给你一个1 + 1 /（1-p1）*（1-p2）形式的等式......

如果你计算每个概率的出现次数 - 看起来你有少量的值会重现 - 你可以使用pow（）函数 - pow（1-p，occurences_of_p）* pow（1 -q，occurrences_of_q） - 并避免每次乘法的单独舍入。

Answer 5

您可以使用概率百分比或promiles：

doc_spam_prob= (numerator*100/(denom1+denom2));

或

doc_spam_prob= (numerator*1000/(denom1+denom2));

或使用其他系数

Answer 6

我的数学能力不强，所以我无法对可能消除或减少问题的公式进行简化评论。但是，我熟悉long double类型的精度限制，并且知道C的几个任意和扩展的精度数学库。退房：

http://www.nongnu.org/hpalib/ 和 http://www.tc.umn.edu/~ringx004/mapm-main.html