在网格中使用顶点（2D和3D）查找边缘的算法

Question

我有一个网格，有某些类型的元素（例如三角形，四边形）。对于每个元素，我知道它的所有顶点，即三角形2D元素将具有3个顶点v1，v2和v3，其x，y，z坐标是已知的。

问题1

我正在寻找一种能够返回所有边缘的算法......在这种情况下：

边缘（v1，v2），边缘（v1，v3），边缘（v2，v3）。根据每个元素有多少个顶点，算法应该有效地确定边缘。

问题2

我正在使用C ++，那么，存储上述算法返回的边缘信息的最有效方法是什么？例如，我感兴趣的是一个元组（v1，v2），我想用它进行一些计算然后忘记它。

谢谢

Answer 1

您可以使用半边数据结构。

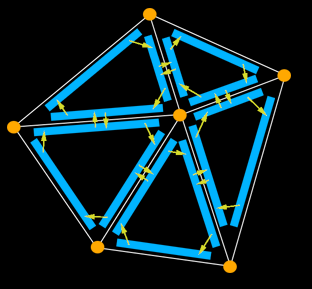
基本上你的网格也有一个边列表，每个方向上每对顶点有一个边缘结构。这意味着如果你有顶点A和B，那么在某处存储两个边缘结构，一个用于A-> B，一个用于B-> A.每个边有3个指针，一个叫做前一个，一个叫做next，一个叫做twin。在下一个和前一个指针之后，您将绕过网格中三角形或多边形的边缘。调用twin会将您带到相邻多边形或三角形中的相邻边缘。 （看看图中的箭头）这是我所知道的最有用和最详细的边缘数据结构。我已经用它来创建新边并更新指针来平滑网格。顺便说一句，每个边缘也应该指向一个顶点，因此它知道它在空间中的位置。

Answer 2

你的问题实际上有三个部分，而不是两个部分：

• 应使用哪些数据结构来表示网格？
• 我应该使用什么算法从网格数据结构中提取边？
• 如何表示生成的边缘集？

您必须提出其他问题才能找到合适的答案。

应该使用哪些数据结构来表示网格？

您需要处理哪些元素类型？

如果你只需要处理多边形（闭环）和单纯形（每个节点连接到元素中的每个其他节点，例如四面体），那么有序节点列表就足够了，因为边缘可以从列表中隐含节点另一方面，如果需要处理六面体，棱镜或一般多面体等元素类型，则需要有关元素拓扑的更多信息。一组简单的边缘映射通常就足够了。它只是元素节点列表中索引的数组[] [2]，告诉你如何连接给定元素类型的点。

Chris描述的半边结构仅适用于2D。在3D中，每个边缘可以有任意数量的元素，而不仅仅是两个。半边缘表示有一个3D扩展，我认为它被称为风车结构。

如果你必须支持任意元素类型，我更喜欢更完整的数据结构来表示元素拓扑。常见的选择是使用边和共边。每对连接节点都有一个边缘结构，并且元素中每个边缘的使用都有一个共边缘。它类似于风车方法，但有点明确。

我应该使用什么算法从元素中提取边缘？

速度或记忆有多重要？结果是每个元素包含一个每个边缘，还是只包含一个元素使用它的一次？结果中边的顺序是否重要？每个边的节点顺序是否重要？

很难想出一种只能访问每个边一次的任意元素类型的算法。为了确保每个边只出现一次，你可以过滤结果，或者你可以有点hackish并在每个边上保持一个“访问”位，以确保你不会在结果中坚持两次。

我应该如何表示结果？

我将如何使用结果？

如果您要在计算密集型计算中使用结果，那么大量坐标可能是最佳选择。您不希望在计算过程中反复重新获取节点坐标。但是，如果您要过滤结果以删除重复边缘，则比较坐标（节点对的6个双精度）不是可行的方法。如果要过滤，首先生成一个指向边结构的指针列表，然后过滤掉重复项，然后然后生成坐标列表。您也可以将此方法用于节点对，但是您必须针对每个边缘的两个可能的节点顺序进行过滤，从而将过滤所需的时间加倍。

如果内存比性能更重要，那么边缘指针列表也是可行的方法。但是，您可以在计算过程中查找坐标，而不是将边列表转换为坐标列表。获取节点坐标的速度较慢，但​​是你要避免制作一个庞大的坐标列表 - 每边存储一个指针而不是每边6个双精度。

许多网格应用程序将所有坐标存储在一个大的全局数组中，每个节点都有一个索引到数组中。如果是这种情况，请将其转换为全局坐标数组中的索引列表，而不是将边列表转换为坐标数组。性能不应该偏离本地坐标数组，但没有内存和人口开销。

Answer 3

我没有适合您的算法，但我可以告诉您在哪里查看。

"Point Set Triangulation"正是您要找的。

以下是一些开源库，可以为您执行此操作（了解算法代码）：

• CGAL的Triangulation_2和Triangulation_3类。
• Triangle（仅限2D）作者：Jonathan Richard Shewchuk
Atul Narkhede和Dinesh Manocha的
• Fast Polygon Triangulation