如何使用boost正态分布类？

Question

我正在尝试使用boost :: normal_distribution来生成平均0和sigma 1的正态分布。

以下代码不起作用，因为某些值超过或超过-1和1（并且不应该）。有人能指出我做错了吗？

#include <boost/random.hpp>
#include <boost/random/normal_distribution.hpp>

int main()
{
  boost::mt19937 rng; // I don't seed it on purpouse (it's not relevant)

  boost::normal_distribution<> nd(0.0, 1.0);

  boost::variate_generator<boost::mt19937&, 
                           boost::normal_distribution<> > var_nor(rng, nd);

  int i = 0; for (; i < 10; ++i)
  {
    double d = var_nor();
    std::cout << d << std::endl;
  }
}

我机器上的结果是：

0.213436
-0.49558
1.57538
-1.0592
1.83927
1.88577
0.604675
-0.365983
-0.578264
-0.634376

如您所见，所有值都不在-1和1之间。

提前谢谢大家！

编辑：当你有最后期限并且在做练习之前避免研究理论时会发生这种情况。

Answer 1

  

以下代码不起作用，因为某些值超过或超过-1和1（并且不应该）。有人能指出我做错了吗？

不，这是对正态分布的标准偏差（构造函数 ¹ 中的第二个参数）的误解。

正态分布是熟悉的钟形曲线。该曲线有效地告诉您值的分布。接近钟形曲线峰值的位置的值比远处的值（分布的尾部）更可能。

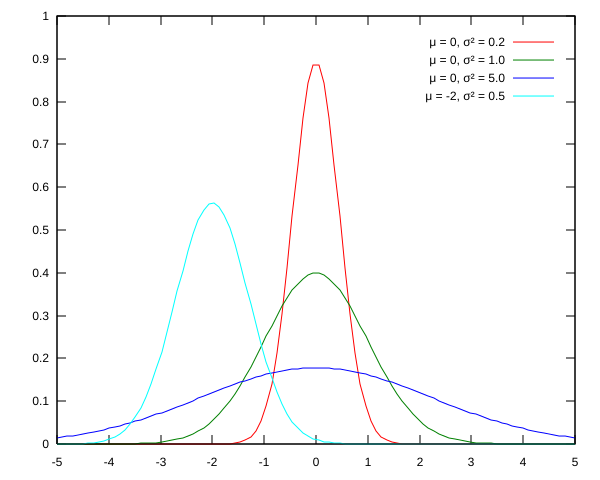
标准偏差告诉您如何展开这些值。数字越小，平均值周围的浓度值就越大。数字越大，均值附近的集中值就越低。在下图中，您会看到红色曲线的方差（方差是标准差的平方）为0.2。将其与具有相同均值但方差为1.0的绿色曲线进行比较。您可以看到绿色曲线中的值相对于红色曲线更加分散。紫色曲线的方差为5.0，数值更加分散。

因此，这解释了为什么值不限于[-1, 1]。然而，一个有趣的事实是，68％的值总是在平均值的一个标准差内。因此，作为一个有趣的测试，你自己编写一个程序，用正态分布绘制大量的值，均值为0，方差为1，并计算均值的一个标准差内的数字。你应该得到接近68％的数字（68.2689492137％更准确一点）。

¹ ：来自提升documentation：

  

normal_distribution(RealType mean = 0, RealType sd = 1);

     

构造具有均值和标准差sd的正态分布。

Answer 2

你没有做错任何事。对于正态分布，sigma指定标准 偏差，而不是范围。如果您生成足够的样本，您将只看到 其中68％位于[mean-sigma，mean + sigma]范围内，2σ内约95％， 并且在3 sigma内超过99％。