100.000向量的有效比较

Question

我在数据库中保存了100.000个向量。每个向量的维数为60.（int vector [60]）

然后我拿一个，并希望当前向量按照与所选择的相似度递减的顺序给用户。

我使用Tanimoto Classifier来比较2个向量：

是否有任何方法可以避免对数据库中的所有条目进行操作？

还有一件事！我不需要对数据库中的所有向量进行排序。我想获得前20名最相似的矢量。所以也许我们可以粗略地控制60％的条目，并使用其余的进行排序。你觉得怎么样？

Answer 1

首先，预处理矢量列表，使每个矢量标准化。单位幅度。 现在请注意，您的比较函数T（）现在具有变为常量的幅度项，并且公式可以简化为查找测试向量与数据库中的值之间的最大点积。

现在，想一个新函数D = 60D空间中两点之间的距离。这是经典的L2 distance，取每个组件的差异，每个组成正方形，添加所有正方形，并取总和的平方根。 D（A，B）= sqrt（（A-B）^ 2）其中A和B各为60维向量。

但是，这可以扩展到D（A，B）= sqrt（A * A -2 *点（A，B）+ B * B）。 那么A和B是单位幅度。函数D是单调的，因此如果我们删除sqrt（）并查看平方距离，它将不会改变排序顺序。这使我们只有-2 *点（A，B）。因此，最小化距离恰好相当于最大化点积。

因此，原始的T（）分类度量可以简化为找到nornalized向量之间的最高点积。并且该比较显示相当于在60维空间中找到最接近的点到采样点。

所以现在你需要做的就是解决“给定60D空间中的归一化点，在数据库中列出最接近它的归一化样本向量的20个点”的等效问题。

这个问题很明显.. K Nearest Neighbors. 有许多算法可以解决这个问题。最常见的是经典KD trees 。

但是有一个问题。 KD树具有O（e ^ D）行为。高维度很快变得痛苦。 60个维度绝对是非常痛苦的类别。不要尝试。

然而，高D最近邻居有几种替代的通用技术。 This paper提供了一个明确的方法。

但在实践中，有一个很好的解决方案涉及另一个转换。如果您有度量空间（您可以使用，或者您不使用Tanimoto比较），则可以通过60维旋转来减少问题的维数。这听起来很复杂和可怕，但它很常见..它是奇异值分解或特征值分解的一种形式。在统计中，它被称为Principal Components Analysis.

基本上，它使用简单的线性计算来查找数据库真正跨越的方向。您可以将60个维度折叠到较低的数字，可能低至3或4，并且仍然能够准确地确定最近的邻居。 有许多软件库可以用任何语言进行，例如，请参阅here。

最后，你会做一个经典的K最近邻居，可能只有3-10个维度。你可以尝试最好的行为。这个名为Ranger的库有一个很棒的库，但你也可以使用其他库。一个很好的附带好处是你甚至不需要再存储样本数据的所有60个组件了！

唠叨的问题是，您的数据是否真的可以折叠到较低维度，而不会影响结果的准确性。在实践中，PCA分解可以告诉您选择的任何D限制的最大残留误差，因此可以确保它有效。由于比较点基于距离度量，因此与哈希表值不同，它们很可能是强相关的。

以上摘要：

1. 规范化矢量，将问题转换为60维的K最近邻问题
2. 使用主成分分析将维度降低到5维的可管理限制
3. 使用K最近邻算法（如Ranger的KD树库）查找附近的样本。

Answer 2

<强>更新

在您明确60是您的空间的维度，而不是向量的长度之后，下面的答案不适用于您，因此我将仅保留历史记录。

---

由于您的向量已标准化，因此您可以使用kd-tree来查找增量超级卷MBH内的邻居。

我知道没有数据库具有kd-tree的本机支持，因此如果您要搜索有限数量的最近条目，您可以尝试在MySQL中实现以下解决方案：

• 将向量的投影存储到2维空间中的每一个（采用n * (n - 1) / 2列）
• 使用SPATIAL索引
为每个列编制索引
• 在任何投影中选择给定区域的正方形MBR。这些MBR的乘积将为您提供一个有限超体积的超立方体，它将保持所有向量的距离不大于给定的值。
• 使用MBR
查找所有MBRContains内的所有投影

你仍然需要在这个有限的价值范围内进行排序。

例如，您有一组4维向量，其幅度为2：

(2, 0, 0, 0)
(1, 1, 1, 1)
(0, 2, 0, 0)
(-2, 0, 0, 0)

您必须按如下方式存储它们：

p12  p13  p14  p23  p24  p34
---  ---  ---  ---  ---  ---
2,0  2,0  2,0  0,0  0,0  0,0
1,1  1,1  1,1  1,1  1,1  1,1
0,2  0,0  0,0  2,0  2,0  0,0
-2,0 -2,0 -2,0 0,0  0,0  0,0

假设您想要与第一个向量(2, 0, 0, 0)大于0的相似性。

这意味着在超立方体中包含向量：(0, -2, -2, -2):(4, 2, 2, 2)。

您发出以下查询：

SELECT  *
FROM    vectors
WHERE   MBRContains('LineFromText(0 -2, 4 2)', p12)
        AND MBRContains('LineFromText(0 -2, 4 2)', p13)
        …

等，适用于所有六列

Answer 3

因此可以缓存以下信息：

• 所选矢量的范数
• 点积A.B，在给定的T（A，B）计算中将其重新用于分子和分母。

如果您只需要N个最接近的向量，或者如果您多次进行相同的排序过程，则可能还有其他技巧可用。 （观察像T（A，B）= T（B，A），缓存所有向量的向量范数，也许还有某种阈值/空间排序）。

Answer 4

为了对某些内容进行排序，您需要为每个项目分类。因此，将至少需要处理每个条目一次以计算密钥。

这是你的想法吗？

======= 在这里发表评论：

鉴于描述，您无法避免查看所有条目来计算您的相似性因子。如果您告诉数据库在“order by”子句中使用相似性因子，您可以让它完成所有艰苦工作。你熟悉SQL吗？

Answer 5

简而言之，不，可能没有办法避免遍历数据库中的所有条目。一个限定词;如果你有大量重复的向量，你可以避免重新处理精确的重复。

Answer 6

较新的回答

你可以做多少预处理？你能提前建立“社区”并注意每个向量在数据库中的哪个社区？这可能会让你从考虑中消除许多向量。

---

下面的旧答案，假设60是所有向量的大小，而不是维度。

由于向量的长度都相同（60），我认为你做的数学太多了。难道你不能只针对每个候选人做出所选产品的点积吗？

在3D中：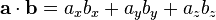

三次乘法。在2D中它只是两个乘法。

或者这是否违反了您的相似性？对我来说，最相似的矢量是它们之间角距最小的矢量。

Answer 7

如果您愿意接受近似值，可以通过几种方法避免在运行时浏览整个数据库。在后台作业中，您可以开始预先计算矢量之间的成对距离。对整个数据库执行此操作是一项巨大的计算，但不需要完成它以使其有用（即，开始计算每个向量的100个随机向量的距离。将结果存储在数据库中）。

然后三角测量。如果你的目标矢量v和某个矢量v'之间的距离d很大，那么v和接近v'的所有其他v'之间的距离也会很大（-ish），所以没有必要比较他们了（你必须自己找到可接受的“大”的定义）。您可以尝试重复丢弃的向量v''的过程，并测试在精度开始下降之前可以避免多少运行时计算。 （制作一组“正确”的比较结果）

祝你好运。

SDS

Answer 8

呃，不是吗？

当然，你只需要对你选择的那个（而不是所有n(n-1)/2个可能的对）做99,999，但这个数量一样低。

---

查看您对nsanders's answer的回复，很明显您已经掌握了这一部分。但我想到了一个特殊情况，计算全套比较可能是一个胜利。如果：

• 列表缓慢进来（比如你从某个数据采集系统以固定的低速率获取它们）
• 直到最后才知道你要与哪个人进行比较
• 你有足够的存储空间
• 当你选择一个时，你需要快速得到答案（天真的方法还不够快）
• 看起来比计算更快

然后您可以在数据进入时预先计算，然后在排序时查找每对结果。如果你最终会做很多种事情，这也可能有效......

Answer 9

没有通过所有条目？这似乎不可能。 你唯一能做的就是在插入时进行数学计算（记住equivalence http://tex.nigma.be/T%2528A%252CB%2529%253DT%2528B%252CA%2529.png：P）。

这可以避免您的查询在执行时针对所有其他列表检查列表（但它可能会大大增加db所需的空间）

Answer 10

对此的另一种看法是具有某些相似性函数的给定阈值的所有对问题。 在这里查看bayardo的论文和代码http://code.google.com/p/google-all-pairs-similarity-search/

我不知道您的相似度函数是否与该方法相匹配，但如果是这样，那么这是另一个要看的方法。在任何情况下，它还需要标准化和排序的向量。