如何确定Delaunay三角形是内部还是外部？

Question

我正在编写一个程序，需要实现Medial Axis提取，其中Delaunay三角测量是一个步骤。外部中轴是不需要的，因此要删除相应的外部三角形。幸运的是，我带着很多图表来到a page，也提示了一种确定内部和外部Delaunay三角形的方法（“基于虚线周长”），但这只是一个提示，没有详细解释。有人知道算法吗？

编辑：我忘了提到从封闭多边形的边界采样的初始点，我的目的是确定每个Delaunay三角形是否在多边形内。

Answer 1

此解决方案假设您有一个数据结构，表示使用“虚拟无限Delaunay顶点”的Delaunay三角剖分，CGAL的方式（see details here）。

想法是找到边界Delaunay边缘：连接两个连续样本点的边缘;然后通过Delaunay三角剖分“泛滥”以对Delaunay面部进行分类。人们知道无限顶点是外部的，因此只要不跨越边界边界，就可以将其邻居（和邻居的邻居等）分类为外部。如果到达边界边缘，可以简单地将相邻三角形标记为内部并继续相似。

输入：封闭形状边界密集采样的点集，甚至可以包含孔 输出：形状内部的Voronoi图（形状的中轴近似）

1. 计算分数的Delaunay三角剖分
2. 标记连接两个连续采样点的Delaunay边。 （参见page 4-5 of this paper如何在每个Delaunay边缘进行本地测试）
3. 将所有无限Delaunay面分类为OUTSIDE并将其推送到队列 Q 。
4. Q 不为空
   1. Delaunay face f =来自 Q
   的流行音乐
   2. 对于f的每个未分类的邻居三角形 t
      • 如果标记 t 和 f 共享的Delaunay边缘， 将 t 归类为 f
      的对立面
      • else分类 t 与 f
      相同
      • 将 t 推送到 Q
5. 对于每个Delaunay边缘 e
   • 如果两个邻居Delaunay三角形 d1 ， d2 都被归类为INTERIOR，则输出连接 d1 和 D2

对于这样的输入

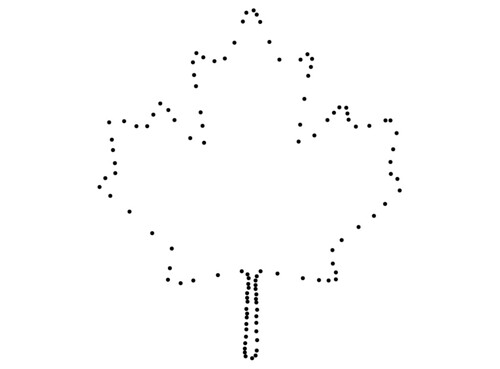
可以计算以下中轴近似值：

您可以使用Mesecina的免费窗口二进制文件检查此中轴近似在实践中的表现。源代码here。

Answer 2

您是否考虑过使用不会创建外部三角形的不同形式的三角测量？我曾经学过一门课程，花了很多时间讨论多边形三角测量的理论方面。也许浏览课程网站会给你一些见解？ http://cgm.cs.mcgill.ca/~godfried/teaching/cg-web.html#triangulation

编辑：实际上，我只想到别的东西。如果你已经有了试图进行三角测量的多边形，你可以使用格林定理。格林定理使用多边形的周长来计算其面积！更重要的是，在这种情况下，您可以通过查看区域的符号来确定点是在线的一侧还是另一侧。在多边形上，格林定理解决了一个简单的减法问题。因此，请知道您知道的是多边形内部，并针对多边形的每个边计算面积。这告诉您每个线的哪一侧需要您的点。现在只需在每个三角形内部取一个点并做同样的事情。如果任何标志错误，那么你有一个外部三角形。 （注意：根据多边形的形状，这可能实际上不起作用。它应该适用于凸多边形，但凹陷可能会引入额外的复杂性。）

Answer 3

也许我在这里做了太多的假设，但听起来你有一个由一堆点组成的多边形，并且你正在对这些点进行三角测量。然后，您想要丢弃多边形之外的所有三角形，对吗？

为什么不对三角形进行三角测量（使用单调分解或类似的东西），以便永远不会创建任何外部三角形？我想这可能会增加运行时间（在O（nlogn）时间内首先进行三角测量，然后在O（n ^ 2）时间内创建一个delaunay三角测量），但可能有更快的方法。

Answer 4

他们提出的算法看起来有点像它们在其中一个数字中显示的那样，这可能是Google学术搜索中似乎没有任何有用引用的原因。

Using their proposed algorithm on a non-convex polygon shows that it does not always recover an actual triangulation. http://www.cc.kyoto-su.ac.jp/~atsushi/Jun/Topics/Teddy/images/example2_2.jpg