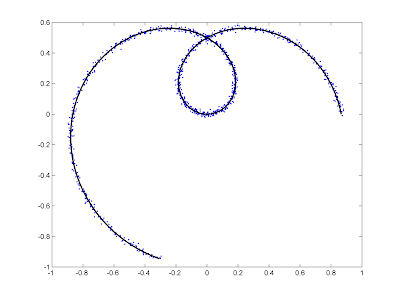
曲线拟合平面上未分类的点

Question

问题：如果曲线不是单值的，那么如何将曲线拟合到平面上的点？

对于所示的示例，如何将曲线（如黑色曲线）与嘈杂的蓝色数据拟合？它类似于样条平滑，但我不知道数据的顺序。

Matlab是首选，但伪代码很好。或者指向这个问题的正确术语的指针会很棒。

由于

Answer 1

您的数据看起来像(x,y)的{​​{1}}，是某些基础参数t的函数。因此，如果您可以为它们提供合理的模型，则可以x(t) y(t)拟合{{1}}和{{1}}。您的数据似乎描述了parametric plot。

Answer 2

编辑：nvm误解了这个问题。无论如何，我会在这里留下这个答案。

也许先尝试找到点的convex hull然后在普通

上拟合凸包

http://www.cse.unsw.edu.au/~lambert/java/3d/giftwrap.html＆lt; - 包括java动画实现 http://en.wikipedia.org/wiki/Convex_hull_algorithms

如果你不想要效率，有一些非常简单的实现，比如礼品包装版本是O（n ^ 2） http://en.wikipedia.org/wiki/Gift_wrapping_algorithm

分而治之的版本是O（nlogn）

Answer 3

您可以尝试推断点的顺序，然后应用样条程序。当然，曲线与自身交叉是模棱两可的。

也许最天真的方法是计算Delaunay三角剖分（nlogn时间），从中近似欧几里德最小距离哈密顿循环通过这些点。您仍然需要弄清楚“结束”的位置。从订购，您可以应用样条技术。有关参考，请参阅Finding Hamiltonian Cycles in Delaunay Triangulations Is NP-Complete，或Reinelt关于TSP启发式，1992年或维基百科EMST的论文

HTH，

Answer 4

对于使用B样条的分段近似，您可以使用this Matlab包。它适用于自动和半手动模式。

Answer 5

我不是专家，但是我发现this page在谈论曲线重建，这似乎很适合您的问题。仍在阅读论文并且很难理解它们，所以我还不能提供解决方案。

Answer 6

你必须做多个分段拟合或样条。不要指望任何算法能够一次完成所有这些。可能至少有三条曲线：第一条到达交叉点，循环，然后从交叉路口向前返回。

Answer 7

如果您没有订购，这个问题真的很难。在某些（x（t），y（t））上进行最小二乘很容易 - 假设您知道 t 的顺序。

你可能需要一些有点搜索算法。遗传算法可能没问题。