图中2个节点之间的所有路径
我必须进行一个不知情的搜索(广度优先搜索)程序,它接受两个节点并返回它们之间的所有路径。
public void BFS(Nod start, Nod end) {
Queue<Nod> queue = new Queue<Nod>();
queue.Enqueue(start);
while (queue.Count != 0)
{
Nod u = queue.Dequeue();
if (u == end) break;
else
{
u.data = "Visited";
foreach (Edge edge in u.getChildren())
{
if (edge.getEnd().data == "")
{
edge.getEnd().data = "Visited";
if (edge.getEnd() != end)
{
edge.getEnd().setParent(u);
}
else
{
edge.getEnd().setParent(u);
cost = 0;
PrintPath(edge.getEnd(), true);
edge.getEnd().data = "";
//return;
}
}
queue.Enqueue(edge.getEnd());
}
}
}
}
我的问题是我只获得了两条路径,而不是所有路径,我不知道在我的代码中编辑什么来获取它们。我的问题输入基于此地图: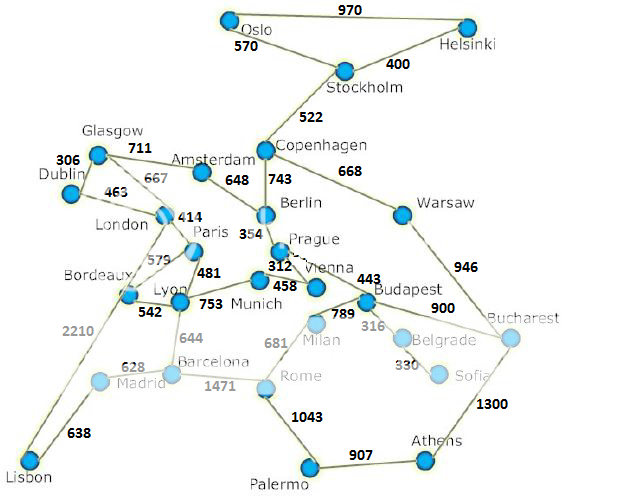
4 个答案:
答案 0 :(得分:3)
广度优先搜索是生成所有可能路径的一种奇怪方式,原因如下:您需要跟踪BFS中的每个单独路径是否已遍历该节点,而不是完全遍历该节点。 / p>
举一个简单的例子
1----2
\ \
3--- 4----5
我们希望所有路径从1到5.我们排队1,然后是2和3,然后是4,然后是5.我们已经失去了有两条路径通过4到5的事实。
我建议尝试使用DFS进行此操作,尽管这可能可以通过一些思考来解决BFS问题。排队的每个东西都是路径,而不是单个节点,因此可以看到该路径是否访问过每个节点。这是浪费的记忆,你是
答案 1 :(得分:3)
在BFS算法中,找到解决方案后一定不能停止。一个想法是为你访问过的所有城市设置数据null,除了第一个,让函数运行一点点。我没有时间给你写一个片段,但如果你没有得到它,我将写至少一个伪代码。如果你没有理解我的想法发表你的问题的评论,我会尝试更好地解释。
答案 2 :(得分:2)
路径是一系列顶点,其中没有顶点重复多次。根据这个定义,你可以编写一个递归算法,它应该按如下方式工作:将四个参数传递给函数,称之为F(u, v, intermediate_list, no_of_vertices),其中u是当前的源(当我们递归时它会改变), v是目的地,intermediate_list是一个最初应为空的顶点列表,每次我们使用顶点时,我们都会将其添加到列表中,以避免在多次使用顶点时使用顶点我们的路径no_of_vertices是我们想要找到的路径的长度,它应该由2下限,上限由V,顶点数量限定。本质上,该函数应返回一个路径列表,其源为u,目的地为v,每条路径的长度为no_of_vertices。创建一个初始空列表并调用F(u, v, {}, 2), F(u, v, {}, 3), ..., F(u, v, {}, V),每次将F的输出与我们打算存储所有路径的列表合并。尝试实现这一点,如果你仍然遇到麻烦,我会为你编写伪代码。
编辑:使用BFS解决上述问题:广度优先搜索是一种可用于探索图形的所有状态的算法。您可以使用BFS浏览给定图形的所有路径的图形,并选择所需的路径。对于每个顶点v,将以下状态添加到队列中:(v, {v}, {v}),其中每个状态定义为:(current_vertex, list_of_vertices_already_visited, current_path)。现在,当队列不为空时,如果尾部顶点e尚未存在,则弹出队列的顶部元素,对于current_vertex的每个边x。 list_of_vertices_already_visited,将新状态(x, list_of_vertices_already_visited + {x}, current_path -> x)推送到队列,并在将其从队列中弹出时处理每个路径。这样,您可以搜索图表的整个路径图,无论是有向还是无向。
答案 3 :(得分:0)
听起来像是家庭作业。但有趣的是。
以下是伪代码,首先是深度而不是先呼吸(所以应该转换为队列类型算法,并且可能包含错误,但是一般的jist应该是清楚的。
class Node{
Vector[Link] connections;
String name;
}
class Link{
Node destination;
int distance;
}
Vector[Vector[Node]] paths(Node source, Node end_dest, Vector[Vector[Node]] routes){
for each route in routes{
bool has_next = false;
for each connection in source.connections{
if !connection.destination in route {
has_next = true;
route.push(destination);
if (!connection.destination == end_dest){
paths(destination, end_dest, routes);
}
}
}
if !has_next {
routes.remove(route) //watch out here, might mess up the iteration
}
}
return routes;
}
编辑:这实际上是您正在寻找的问题的答案吗?或者你真的想找到最短路径?如果是后者,请使用Dijkstra的算法:http://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
- 我写了这段代码,但我无法理解我的错误
- 我无法从一个代码实例的列表中删除 None 值,但我可以在另一个实例中。为什么它适用于一个细分市场而不适用于另一个细分市场?
- 是否有可能使 loadstring 不可能等于打印?卢阿
- java中的random.expovariate()
- Appscript 通过会议在 Google 日历中发送电子邮件和创建活动
- 为什么我的 Onclick 箭头功能在 React 中不起作用?
- 在此代码中是否有使用“this”的替代方法?
- 在 SQL Server 和 PostgreSQL 上查询,我如何从第一个表获得第二个表的可视化
- 每千个数字得到
- 更新了城市边界 KML 文件的来源?