绘制旋转矩形

Question

我意识到这可能更像是一个数学问题。

要为我的矩形绘制线条，我需要解决它们的角落。 我在（x，y）处有一个矩形中心，带有定义的宽度和高度。

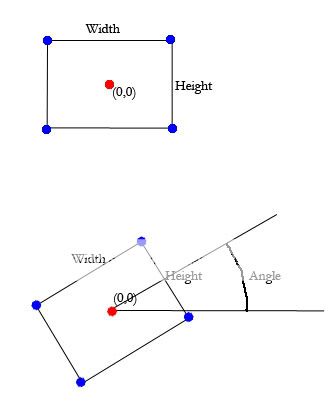
在顶部的非旋转矩形上找到蓝点（角度= 0） 是

UL = (x-Width/2),(y+height/2)
UR = (x+Width/2),(y+height/2)
LR = (x+Width/2),(y-height/2)
LL = (x-Width/2),(y-height/2)

如果角度不是0，我如何找到点？

提前致谢。

<小时/> 更新：虽然我的图片中有（0,0）作为中心点，但中心点很可能不在该位置。

Answer 1

首先将中心点转换为0,0

X'= X-x

Y'= Y-y

然后旋转角度A

X''=（X-x）* cos A - （Y-y）* sin A

Y''=（Y-y）* cos A +（X-x）* sin A

再次将中心点转换回x，y

X'''=（X-x）* cos A - （Y-y）* sin A + x

Y'''=（Y-y）* cos A +（X-x）* sin A + y

因此，使用以下变换计算（X，Y）的所有4个点

X'''=（X-x）* cos A - （Y-y）* sin A + x

Y'''=（Y-y）* cos A +（X-x）* sin A + y

其中x，y是矩形的中心点，X，Y是角点 如果我在评论中给出了Angle为0，你甚至没有正确定义角点。

替换后你会得到

UL  =  x + ( Width / 2 ) * cos A - ( Height / 2 ) * sin A ,  y + ( Height / 2 ) * cos A  + ( Width / 2 ) * sin A
UR  =  x - ( Width / 2 ) * cos A - ( Height / 2 ) * sin A ,  y + ( Height / 2 ) * cos A  - ( Width / 2 ) * sin A
BL =   x + ( Width / 2 ) * cos A + ( Height / 2 ) * sin A ,  y - ( Height / 2 ) * cos A  + ( Width / 2 ) * sin A
BR  =  x - ( Width / 2 ) * cos A + ( Height / 2 ) * sin A ,  y - ( Height / 2 ) * cos A  - ( Width / 2 ) * sin A

我认为这适合您的解决方案。

Answer 2

如果'theta'是逆时针旋转角度，则旋转矩阵为：

| cos(theta)  -sin(theta) |
| sin(theta)   cos(theta) |

即

x' = x.cos(theta) - y.sin(theta)
y' = x.sin(theta) + y.cos(theta)

如果旋转点不在原点，从原始坐标中减去旋转中心，执行如上所示的旋转，然后重新添加旋转中心。

在http://en.wikipedia.org/wiki/Transformation_matrix

处有其他转换的例子

Answer 3

Rotation matrix （这正成为FAQ）

Answer 4

请参阅2D Rotation。

q = initial angle, f = angle of rotation.

x = r cos q 
y = r sin q

x' = r cos ( q + f ) = r cos q cos f - r sin q sin f 
y' = r sin ( q + w ) = r sin q cos f + r cos q sin f

hence:
x' = x cos f - y sin f
y' = y cos f + x sin f

Answer 5

最简单的方法之一是在旋转前获取点的位置，然后应用坐标变换。由于它以（0,0）为中心，这只是使用的一种情况：

x'= x cos（theta） - y sin（theta）

y'= y cos（theta）+ x sin（theta）

Answer 6

使用这个......我成功了......

 ctx.moveTo(defaults.x1, defaults.y1);

    // Rotation formula
    var x2 = (defaults.x1) + defaults.lineWidth * Math.cos(defaults.rotation * (Math.PI / 180));
    var y2 = (defaults.y1) + defaults.lineWidth * Math.sin(defaults.rotation * (Math.PI / 180));

    ctx.lineTo(x2, y2);

    x2 = (x2) + defaults.lineHeight * Math.cos((defaults.rotation + 90) * (Math.PI / 180));
    y2 = (y2) + defaults.lineHeight * Math.sin((defaults.rotation + 90) * (Math.PI / 180));
    ctx.lineTo(x2, y2);

    x2 = (x2) + defaults.lineWidth * Math.cos((defaults.rotation + 180) * (Math.PI / 180));
    y2 = (y2) + defaults.lineWidth * Math.sin((defaults.rotation + 180) * (Math.PI / 180));
    ctx.lineTo(x2, y2);

    x2 = (x2) + defaults.lineHeight * Math.cos((defaults.rotation + 270) * (Math.PI / 180));
    y2 = (y2) + defaults.lineHeight * Math.sin((defaults.rotation + 270) * (Math.PI / 180));