作为一名程序员，您如何解释想象中的数字？

Question

作为一名程序员，我认为擅长数学是我的工作，但我无法绕过想象中的数字。我试过谷歌和wikipedia没有运气，所以我希望程序员可以向我解释，给我一个数字平方的例子是＆lt; = 0，一些示例用法等...

Answer 1

我想这blog entry是一个很好的解释：

关键字是旋转（与 方向 相反，对于负数，当您想到它们时，它们与虚数一样陌生：少于一切？）

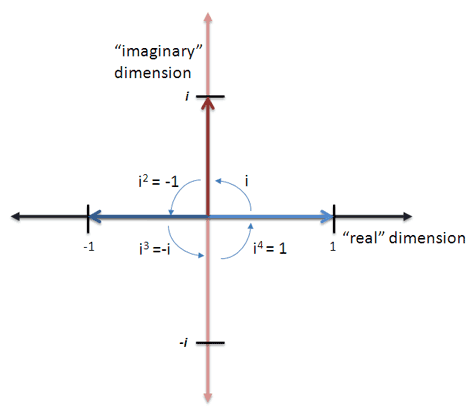
像负数模型翻转一样，虚数可以模拟在两个维度“X”和“Y”之间旋转的任何内容。或任何具有循环，循环关系的东西

Answer 2

问题：我不仅是一名程序员，而且还是一名数学家。 解决方案：无论如何都要向前推。

复杂的数字并没有什么神奇之处。他们成立背后的想法是实数存在问题。如果你有一个方程x ^ 2 + 4，那么它永远不会为零，而x ^ 2 - 2则为零两次。所以数学家真的很生气，并且希望总是用度数至少为1的多项式（想要一个“代数闭合”字段）为零，并创建一些任意数j，使得j = sqrt（-1）。所有的规则都从那里落到了位置（尽管它们更准确地进行了不同的重组 - 具体来说，你们形式上实际上并不能说“嘿，这个数字是负数的平方根”）。如果有那个数字j，你可以得到j的倍数。你可以在j中添加实数，这样你就得到了复数。具有复数的运算类似于使用二项式的运算（故意如此）。

复合体的真正问题不在于所有这些，而在于您无法定义一个系统，您可以通过该系统获得低于和大于的普通规则。所以真的，你到了根本没有定义的地方。它在二维空间中没有意义。所以说实话，我实际上无法回答“给我一个等于＆lt; = 0”的数字的问题，但如果你将它的正方形视为实数而不是复数，则“j”是有意义的。 / p>

至于用途，我个人在使用分形时最常使用它们。 mandelbrot分形背后的想法是它是一种绘制z = z ^ 2 + c及其沿实虚轴的发散的方式。

Answer 3

您可能也会问为什么存在负数？它们的存在是因为你想要表示某些方程的解，例如：x + 5 = 0.同样的事情适用于虚数，你想要紧凑地表示形式方程的解：x ^ 2 + 1 = 0。

这是我看到它们在实践中使用的一种方式。在EE中，您经常处理的是正弦波或可以分解为正弦波的函数。 （例如参见Fourier Series）。

因此，您经常会看到形式方程式的解决方案：

f（t）= A * cos（wt）

此外，通常您希望表示通过此功能从某个阶段移位的函数。 90度相移会给你一个sin函数。

g（t）= B * sin（wt）

通过组合这两个函数（称为同相和正交分量），可以获得任意相移。

h（t）= A cos（wt）+ i B * sin（wt）

这里的关键是在线性系统中：如果f（t）和g（t）求解方程式，h（t）也将求解相同的方程式。所以，现在我们有一个通用的方程式h（t）。

关于h（t）的好处是它可以紧凑地编写为

h（t）= Cexp（wt + theta）

使用exp（iw）= cos（w）+ i * sin（w）的事实。

这一切都没有什么特别深刻的东西。它只是利用数学身份来紧凑地表示各种方程的通用解。

Answer 4

嗯，对程序员来说：

class complex {
public:
  double real;
  double imaginary;

  complex(double a_real) : real(a_real), imaginary(0.0) { }
  complex(double a_real, double a_imaginary) : real(a_real), imaginary(a_imaginary) { }

  complex operator+(const complex &other) {
    return complex(
        real + other.real,
        imaginary + other.imaginary);
  }
  complex operator*(const complex &other) {
    return complex(
        real*other.real - imaginary*other.imaginary,
        real*other.imaginary + imaginary*other.real);
  }

  bool operator==(const complex &other) {
    return (real == other.real) && (imaginary == other.imaginary);
  }
};

基本上就是这一切。复数只是实数对，为此定义了+，*和==的特殊重载。而这些操作实际上只是像这样定义了 。然后事实证明，这些操作的数字对与其余的数学很好地匹配，因此它们得到一个特殊的名称。

它们不是像“计数”那么多的数字，但更像是“可以用+， - ，*，...操纵，并且在与'常规'数字混合时不会引起问题”。它们很重要，因为它们填充了实数留下的孔，就像没有正方形为-1的数字一样。现在你有complex(0, 1) * complex(0, 1) == -1.0这是一个有用的符号，因为在这些情况下你不必特别处理负数。 （并且，事实证明，当您使用复数时，基本上不再需要所有其他特殊情况）

Answer 5

如果问题是“存在虚数吗？”或“虚数如何存在？”那对程序员来说这不是一个问题。它甚至可能不是一个数学家的问题，而是一个形而上学家或数学哲学家，尽管数学家可能觉得有必要证明他们在这个领域的存在。从数量存在的讨论开始是很有用的（很多接近这个问题的数学家都是柏拉图主义者，fyi）。有些人坚持认为，想象中的数字（正如怀特黑德所做的那样）是一种实用的便利。但是，如果想象的数字仅仅是一种实际的便利，那对数学有什么看法呢？你不能简单地将想象数字解释为仅仅是实用工具或一对实数，而不必考虑它们和它们“实用”的一般后果。其他人坚持想象数的存在，认为它们的不存在会破坏大量使用它们的物理理论（QM在复杂的希尔伯特空间中是膝盖深的）。我相信这个问题超出了本网站的范围。

如果您的问题更具实际意义，例如：如何在软件中表达虚数，然后上面的答案（一对实数，以及它们的定义操作）就是它。

Answer 6

重点是你将定义的数字添加为二次方程的解，如x ² = -1。为该等式i命名一个解，i的计算规则从该等式得出。

这类似于将负数定义为2 + x = 1等方程式的解，当你只知道正数时，或者当你只知道整数时，分数就像2x = 1那样的方程的解。

Answer 7

最简单的方法是停止尝试理解 数字如何成为负数的平方根，并继续假设它是。

所以（使用 i 作为-1的平方根）：

(3+5i)*(2-i)
= (3+5i)*2 + (3+5i)*(-i)
= 6 + 10i -3i - 5i * i
= 6 + (10 -3)*i - 5 * (-1)
= 6 + 7i + 5
= 11 + 7i

根据数学的标准规则工作（记住我在第四行的平方等于-1）。

Answer 8

虚数是实数乘以虚数单位i。 i定义为：

i == sqrt(-1)

所以：

i * i == -1

使用此定义，您可以获得负数的平方根，如下所示：

   sqrt(-3)
== sqrt(3 * -1)
== sqrt(3 * i * i) // Replace '-1' with 'i squared'
== sqrt(3) * i     // Square root of 'i squared' is 'i' so move it out of sqrt()

您的最终答案是实数sqrt(3)乘以虚数单位i。

Answer 9

一个简短的回答：实数是一维的，虚数加上方程的第二维，如果你乘以一些奇怪的东西......

Answer 10

如果您对查找简单的应用程序感兴趣，并且熟悉矩阵， 在复杂空间中使用复数将一个完美的真实矩阵变换成三角形矩阵有时很有用，它使计算更容易。

结果当然是完全真实的。

Answer 11

到目前为止很棒的答案（真的像Devin的！）

还有一点：

复数的最初使用之一（虽然当时没有这样称呼）是解决3度方程的中间步骤。 link

同样，这纯粹是一种用来回答具有物理意义的真实数字的实际问题的工具。

Answer 12

我不想把这个网站变成数学溢出，但对于那些感兴趣的人：查看Paul J. Nahin撰写的“一个虚构的故事：sqrt（-1）的故事”。它以有趣和令人兴奋的方式讨论了虚数的所有历史和各种应用。这本书让我在7年前读到它时决定攻读数学学位（我正在思考艺术）。好读！!!

Answer 13

在电气工程中，电感器的阻抗Z是jwL，其中w = 2 * pi * f（频率），j（sqrt（-1））表示它导致90度，而对于电容器Z = 1 / jwc = -j / wc，它是-90deg / wc，因此它会使一个简单的电阻滞后90度。