Ortho和Persp正在反转Z深度符号？

Question

用于OpenGL的NDC坐标形成一个立方体，-Z一侧压在屏幕上，而+Z一侧则最远。

当我使用...

// ortho arguments are: left, right,  bottom, top,  near, far
pos = pos * glm::ortho<float>(-1, 1, -1, 1, -1, 1);

...反映了z的{​​{1}}组件； -1变成1，10变成-10，依此类推

glm :: persp做类似的事情，有点奇怪吗？如果某个位置的pos等于z，我希望它停留在NDC立方体面向屏幕的平面上，但是它的符号被任意翻转了；它甚至没有降落到最远的一面。

这是为什么？

Answer 1

  

用于OpenGL的NDC坐标形成一个立方体，它的-Z侧按压屏幕，而+ Z侧最远。

我浏览了Song Ho Ahns有关OpenGL转换的教程，以确保不要讲傻话。

Perspective Projection

  

在透视投影中，将截头截头锥体的3D点（眼睛坐标）映射到立方体（NDC）； x坐标从[l，r]到[-1，1]的范围，y坐标从[b，t]到[-1，1]的范围，z坐标从[-n，-f]的范围到[-1，1]。

     

请注意，眼睛坐标是在右手坐标系中定义的，但是 NDC使用左手坐标系。也就是说，原点的相机在眼睛空间中沿-Z轴方向观察，而在NDC中则沿+ Z轴方向进行观察。

（强调是我的。）

他为此提供了以下很好的说明：

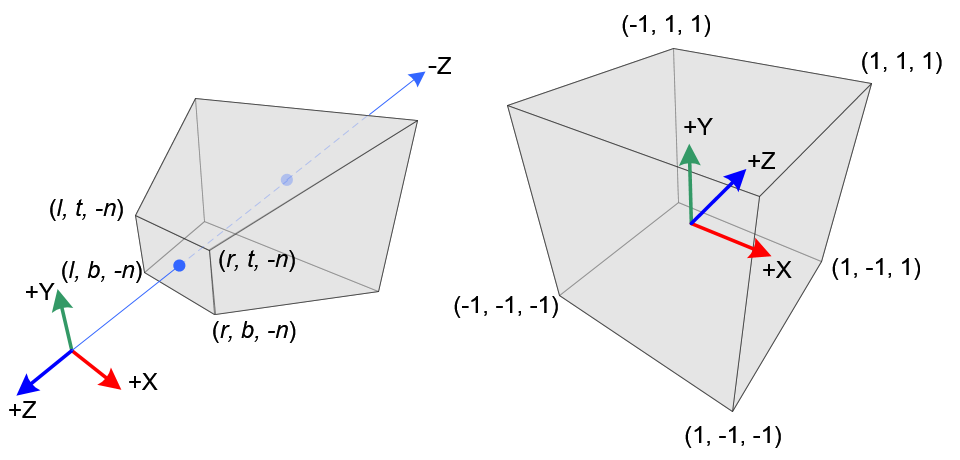
所以，我得出的结论是

glm::ortho<float>(-1, 1, -1, 1, -1, 1);

不应产生单位矩阵，而应产生z轴镜像的矩阵，例如像

|  1  0  0  0 |
|  0  1  0  0 |
|  0  0 -1  0 |
|  0  0  0  1 |

由于手头没有glm，因此从github（glm）的源代码中提取了相关的代码行。在源代码中花了一段时间，我终于在orthoLH_ZO()中找到了glm::ortho()的实现：

template<typename T>
GLM_FUNC_QUALIFIER mat<4, 4, T, defaultp> orthoLH_ZO(T left, T right, T bottom, T top, T zNear, T zFar)
{
    mat<4, 4, T, defaultp> Result(1);
    Result[0][0] = static_cast<T>(2) / (right - left);
    Result[1][1] = static_cast<T>(2) / (top - bottom);
    Result[2][2] = static_cast<T>(1) / (zFar - zNear);
    Result[3][0] = - (right + left) / (right - left);
    Result[3][1] = - (top + bottom) / (top - bottom);
    Result[3][2] = - zNear / (zFar - zNear);
    return Result;
}

我对代码进行了一些转换，以使其成为以下示例：

#include <iomanip>
#include <iostream>

struct Mat4x4 {
  double values[4][4];
  Mat4x4() { }
  Mat4x4(double val)
  {
    values[0][0] = val; values[0][1] = 0.0; values[0][2] = 0.0; values[0][3] = 0.0;
    values[1][0] = 0.0; values[1][1] = val; values[1][2] = 0.0; values[1][3] = 0.0;
    values[2][0] = 0.0; values[2][1] = 0.0; values[2][2] = val; values[2][3] = 0.0;
    values[3][0] = 0.0; values[3][1] = 0.0; values[3][2] = 0.0; values[3][3] = val;
  }
  double* operator[](unsigned i) { return values[i]; }
  const double* operator[](unsigned i) const { return values[i]; }
};

Mat4x4 ortho(
  double left, double right, double bottom, double top, double zNear, double zFar)
{
  Mat4x4 result(1.0);
  result[0][0] = 2.0 / (right - left);
  result[1][1] = 2.0 / (top - bottom);
  result[2][2] = - 1;
  result[3][0] = - (right + left) / (right - left);
  result[3][1] = - (top + bottom) / (top - bottom);
  return result;
}

std::ostream& operator<<(std::ostream &out, const Mat4x4 &mat)
{
  for (unsigned i = 0; i < 4; ++i) {
    for (unsigned j = 0; j < 4; ++j) {
      out << std::fixed << std::setprecision(3) << std::setw(8) << mat[i][j];
    }
    out << '\n';
  }
  return out;
}

int main()
{
  Mat4x4 matO = ortho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0);
  std::cout << matO;
  return 0;
}

编译并启动后，将提供以下输出：

   1.000   0.000   0.000   0.000
   0.000   1.000   0.000   0.000
   0.000   0.000  -1.000   0.000
  -0.000  -0.000   0.000   1.000

Live Demo on coliru

呵呵！ z用-1缩放，即z值在x-y平面上镜像（如预期）。

因此，OP的观察是完全正确和合理的：

  

...反映了pos的z分量； -1变成1，10变成-10，依此类推。

---

最困难的部分：

  

这是为什么？

我个人的猜测：发明了所有这些GL东西的SGI大师之一，都是按照她/他的明智之举做到这一点的。

另一个猜测：在眼部空间中，x轴指向右，y轴指向上。将其转换为屏幕坐标后，y轴应指向下方（因为通常/技术上是从左上角开始对像素进行寻​​址）。因此，这引入了另一个镜像轴，该轴再次改变了坐标系的手性。

这有点令人不满意，因此我在Google上搜索并发现了此信息（重复吗？）：

SO: Why is the Normalized Device Coordinate system left-handed?