迷宫生成算法,我可以选择入口和出口点
什么是一个好的迷宫生成算法,开发人员可以任意选择入口和出口点(当然,它们都应位于边缘)?一段伪代码或任何语言的实现都是最有帮助的。
3 个答案:
答案 0 :(得分:1)
虽然不完全是算法,但我在这里描述了创建迷宫的一些步骤。每个步骤都需要转换为代码,但我认为它们是一个很好的起点。
稍后,将会切割其中一些墙壁,例如创建路径。
在下图中,将切割将与路径相交的每个墙;
所有未被任何路径切割的墙都将被保留。
步骤1:我们从以下方式开始:在入口点和出口点之间创建最简单的路径;这个 路径将只由一条水平线和一条垂直线组成。
接下来,因为这条路太简单了,所以我们试着让它更复杂(扭曲更多,转弯更多);我们这样做 逐渐替换现有路径的段,矩形的三个边(其中, 与删除的段一起,将代表整个矩形);我们重复一遍 根据需要多次步行,只注意路径不会自相交。
步骤2:现在我们有一条相对复杂的路径连接迷宫中的入口和出口点。 然而,矩阵中仍有细胞,四面都有围绕它们的墙壁。我有 寻找一些迷宫的例子,我注意到迷宫中的每个细胞都是潜在的 从入口点可以进入,即使它是一个死胡同。 (换句话说,所有的 迷宫中的路径形成一棵树。)
我们现在需要做的是连接所有剩余的单元格 迷宫到现有的道路。作为惯例,我将打电话给主要路径'我们刚刚创建的路径 从入口到出口点;分支出来的所有其他路径将被命名为“辅助” 路径&#39 ;.那么我们如何创建次要路径?通过在迷宫的大区域中挑选一个随机点 不是主路径遍历的,而是主路径上的另一个随机点。比连接这些点 与进入和退出点类似的方式:用最简单的路径链接它们,稍后制作 这条路径更复杂 - 通过用3个段替换一个段来构成a的补码 长方形。我们不需要多次重复此步骤,因为次要路径不需要更复杂 而不是主要的道路。
步骤3:现在我们已经创建了几个辅助路径,通过将迷宫中的一些随机点与主路径相关联。 仍然有一些区域无法进入,但它们很小。所以对于这些细胞,我们可以将它们联系起来 一条直线到主路径或次要路径中的最近点,就是它。所有的方块 在迷宫中是可以访问的。我们现在需要做的就是移除任何与路径相交的墙,并保留所有墙 其他墙壁。
答案 1 :(得分:0)
有很多算法可以生成迷宫:我希望你可以通过一些工作来改变它们,以便指定起点和终点。
我对迷宫了解的最佳参考是Jamis Buck的Mazes For Programmers。 Jamis blogs about many things software-related,在他的帖子中你可以找到很多迷宫算法。以下是对他博客中的内容的回顾:
-
- 将第一行的单元格初始化为各自的单元格。
- 现在,随机连接相邻的单元格,但前提是它们不在同一个集合中。连接相邻单元格时,将两组单元格合并为一组,表示两组中的所有单元格现已连接(有一条连接集合中任意两个单元格的路径)。
- 对于每个集合,随机向下创建垂直连接到下一行。每个剩余的集合必须至少有一个垂直连接。这样连接的下一行中的单元格必须共享它们上面的单元格集。
- 通过将任何剩余的单元格放入自己的集合中来充实下一行。
- 重复,直到到达最后一行。
- 对于最后一行,加入所有不共享集合的相邻单元格,并省略垂直连接,然后就完成了!
-
- 将图表中的所有边缘扔进一个大麻布袋中。 (或者,你知道,一套或什么的。)
- 拉出重量最轻的边缘。如果边连接两个不相交的树,则加入树。否则,抛开那边。
- 重复,直到没有剩余边缘。
-
- 从G(图表)中选择一个任意顶点,并将其添加到某些(最初为空)集合V中。
- 从G中选择权重最小的边,将V中的顶点与不在V中的另一个顶点连接起来。
- 将该边添加到最小生成树,将边的另一个顶点添加到V。
- 重复步骤2和3,直到V包含G中的每个顶点。
-
- 以空场开始。
- 水平或垂直用墙隔平场。在墙上添加一条通道。
- 使用墙壁两侧的区域重复步骤#2。
- 递归继续,直到迷宫达到所需的分辨率。
-
- 在字段中选择一个起点。
- 在该点随机选择一条墙并雕刻到相邻单元格的通道,但前提是尚未访问相邻单元格。这成为新的当前单元格。
- 如果访问了所有相邻的单元格,请备份到最后一个没有墙壁的单元格并重复。
- 当流程一直支持到起点时,算法结束。
-
- 选择一个顶点。任何顶点。
- 选择顶点的连接邻居并前往它。如果尚未访问邻居,请将行进边缘添加到生成树。
- 重复步骤2,直到访问过所有顶点。
-
- 随机选择任何顶点并将其添加到UST。
- 选择UST中尚未存在的任何顶点并执行随机漫步,直到遇到UST中的顶点。
- 将随机游走中触及的顶点和边缘添加到UST。
- 重复2和3,直到所有顶点都添加到UST。
-
- 选择一个起始位置。
- 进行随机游走,将通道雕刻到未见过的邻居,直到当前的小区没有未访问的邻居。
- 进入“搜索”模式,您可以在其中扫描网格,查找与访问过的单元格相邻的未访问单元格。如果找到,在两者之间划出一条通道,让以前未经检查过的单元成为新的起始位置。
- 重复步骤2和3,直到搜索模式扫描整个网格并找不到未访问的单元格。
-
- 设C为单元格列表,最初为空。随机地向C添加一个单元格。
- 从C中选择一个单元格,并向该单元格的任何未访问的邻居创建一个段落,同时将该邻居添加到C中。如果没有未访问的邻居,请从C中删除该单元格。
- 重复#2直到C为空。
-
- 对于网格中的每个单元格,随机地向北或向西雕刻一条通道。
- 是的,那就是它。
-
- 逐行完成网格,从0,0处的单元格开始。将“运行”设置初始化为空。
- 将当前单元格添加到“运行”集。
- 对于当前单元格,随机决定是否向东雕刻。
- 如果刻有一个通道,则将新单元格设为当前单元格并重复步骤2-4。
- 如果没有雕刻通道,请选择运行中的任何一个单元格并向北刻一条通道。然后清空运行集,将行中的下一个单元格设置为当前单元格,然后重复步骤2-5。
- 继续,直到处理完所有行。
祝你好运。
答案 2 :(得分:0)
对于从任何平面图生成随机迷宫的实现,请签出this web app。为了对此稍有不同,以及对偶图的一般描述,我也将a presentation组合在一起。
请注意,进入或退出的概念是我完全没有解决的。但是,在定义明确的迷宫中,您始终可以将入口和出口点放置在任何位置。 (当然,有些解决方案可能会导致琐碎的遍历。)在任何迷宫中,您应该始终能够在任意两个点或“房间”之间旅行。
在给定特定迷宫的情况下,找到导致有趣或足够复杂的解决方案的入口和出口点,很可能只是确保解决方案具有足够的长度。如果您要预先指定任意图形的入口,则还可以非常简单地完成此操作。
如果您有一个图形并且想要添加起点或终点,那么您所要做的就是在外围添加一个“房间”。这个房间必须可以到达迷宫的其余部分,并且只能通过移开它和迷宫的其余部分之间的墙才能到达。想法如下所示,起始和结束房间分别为左上角和右下角的三角形:
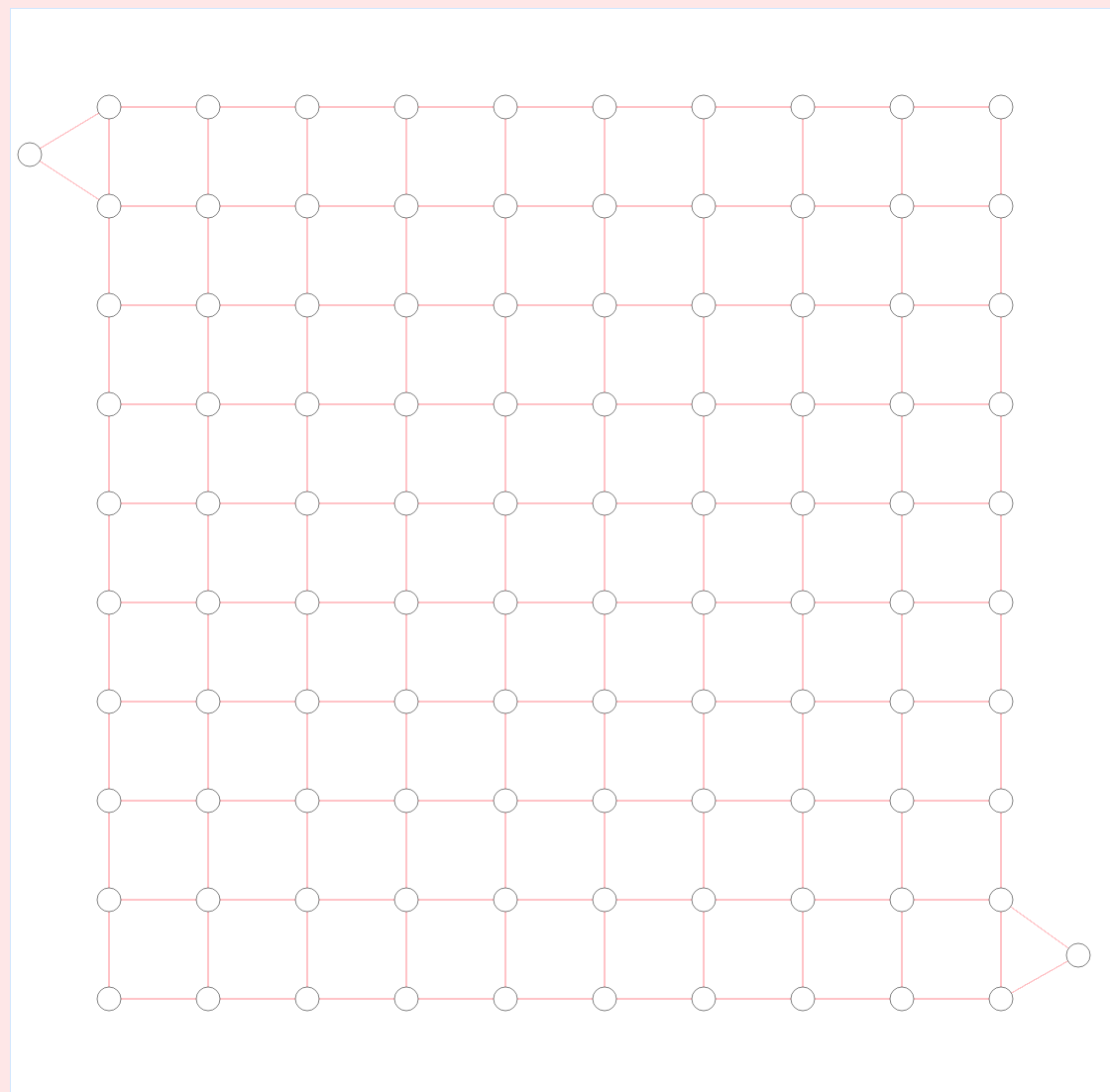 。
。
图中的随机迷宫如下:
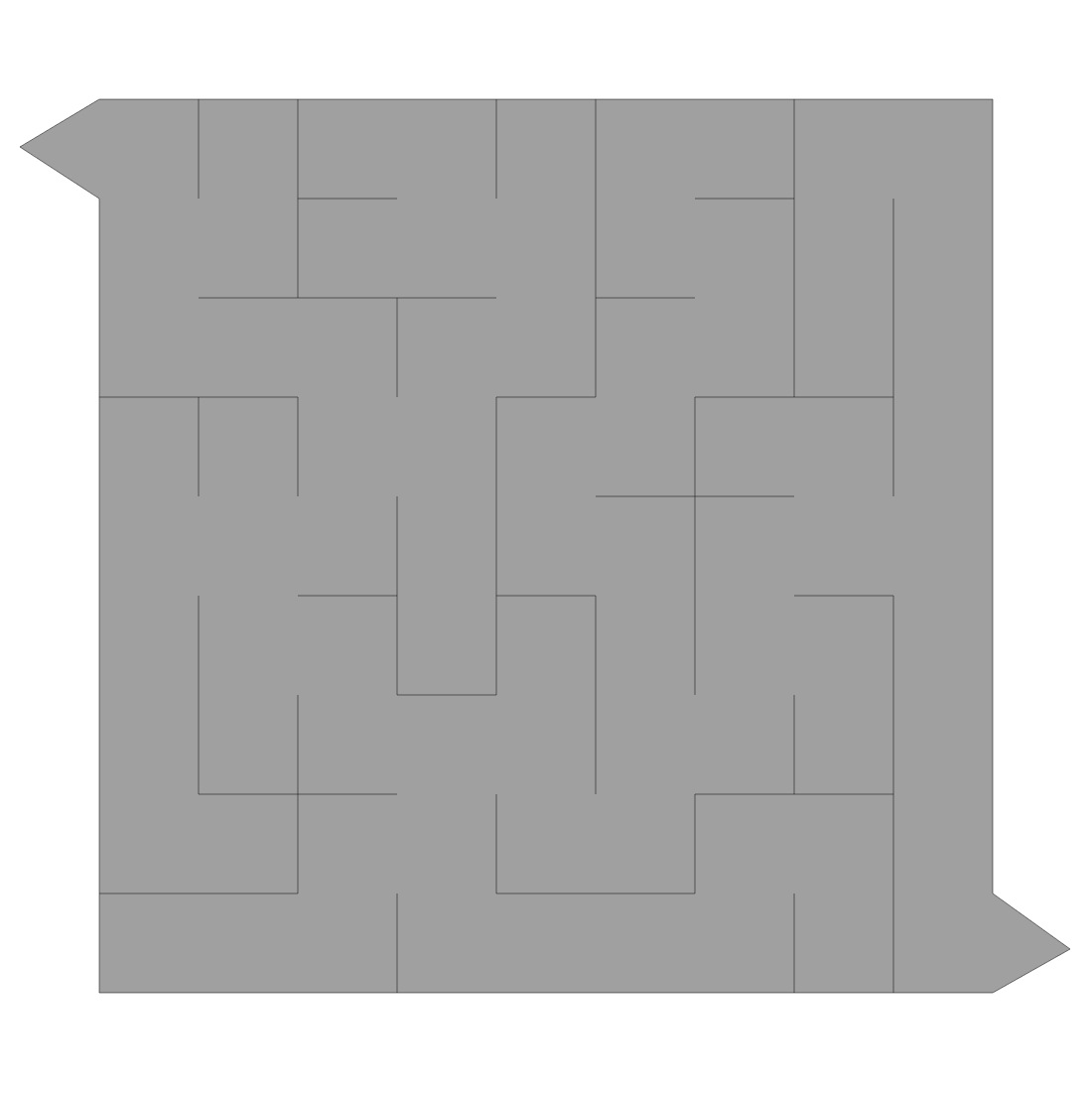
- 我写了这段代码,但我无法理解我的错误
- 我无法从一个代码实例的列表中删除 None 值,但我可以在另一个实例中。为什么它适用于一个细分市场而不适用于另一个细分市场?
- 是否有可能使 loadstring 不可能等于打印?卢阿
- java中的random.expovariate()
- Appscript 通过会议在 Google 日历中发送电子邮件和创建活动
- 为什么我的 Onclick 箭头功能在 React 中不起作用?
- 在此代码中是否有使用“this”的替代方法?
- 在 SQL Server 和 PostgreSQL 上查询,我如何从第一个表获得第二个表的可视化
- 每千个数字得到
- 更新了城市边界 KML 文件的来源?



