拥有最终的Thiessen多边形，是否有可能找到最初的点集？

Question

我试图找到一种方法来反转Voronoi算法。

基本上，有一些连接的形状，主要由三角形和正方形组成，我试图找到一组点，通过使用Voronoi算法将重建初始形状。

Answer 1

<强>简介 在Ash和Boker于1985年部分解决之后，2013年Biedl et al.在一篇论文中解决了这个问题。如果您的Voronoi节点都是奇数度，那么Ash和Bolker的算法适合您。

首先请注意，可能没有 点集，但许多点集都具有您要求的相同Voronoi图。例如，考虑这张图片

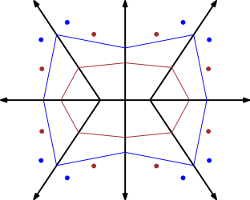
取自this website。红点设置和蓝点设置为您提供相同的黑色Voronoi图。 （顺便说一下，红色和蓝色多边形的straight skeletons也与点集的Voronoi图重合。）

算法概述。 粗略的想法如下。假设一个oracle告诉你Voronoi细胞中的一个候选点。然后，您可以通过相邻单元格之间的公共边缘将此点镜像到相邻的Voronoi单元格，并继续传播。

但可能会遇到麻烦：镜像点可能位于相邻小区之外。此外，如果您考虑Voronoi节点和入射单元，那么您可以通过入射Voronoi边缘继续围绕一个周期传播该点，但是您可能不会再次在原始点处结束。

所以论文的作用如下：

• 它为您的输入提供了足够和必要的条件，以形成Voronoi图。

• 它告诉您如果存在这样的点，如何选择有效的起点。实际上，它为您提供了所有可能的起点。

第二部分大致如下工作：对于每个Voronoi单元，人们都知道＆＃34;区域＆＃34;通过调查细胞的Voronoi节点，必须说明这一点。然后采用Voronoi图的双图的生成树并选择任意根。对于每个单元格，您都拥有独特的镜像路径＆＃34;到＆＃34;根细胞＆＃34;。应用上述区域的镜像序列并与镜像相交。

交叉点是所有可能起点的集合。如果它是空的，那么你的输入不是Voronoi图。

进一步简化。 如果你的Voronoi节点是奇数度，那么问题就更简单了。考虑Biedl等人的论文中的图-4。为每个节点找出点必须位于的线。如果Voronoi单元具有两个奇数度的节点，则可以将这些线交叉并获得单个可能的候选点。您可以为每个Voronoi单元执行此操作。

Answer 2

找不到每个三角形的质心会给你一个根据定义的点，尽可能远离其他点。