Question

我有一个数学问题，写得像这样：

x^1+x^2+x^3+...+x^n

C＃中是否有任何构造可以帮助我解决这些方程？

我知道我可以写一个for循环或使用递归来完成这个，但是我记得在c＃中读到一些预编译这样一个语句以便以后执行的构造。

有没有什么有趣的方法可以解决这些方程？

Answer 1

要计算x ^ n，请使用Math.Pow：

Math.Pow(x, n)

如果要计算总和，可以使用循环或LINQ。我不认为这里有一个简单的循环有什么问题：

double total = 0;
for (int i = 1; i <= n; ++i)
{
    total += Math.Pow(x, i);
}
Console.WriteLine(total);

你可以在LINQ中写这个，但我没有看到任何特别强烈的理由这样做。也许您可以扩展您正在寻找的功能？你在寻找更好的表现吗？

由于您的问题被标记为“数学优化”，您可能还希望通过查找快捷方式对其进行优化。在这种特定情况下，它是geometric series，因此您可以使用以下公式：

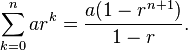
$alt text$

或者在C＃中：

static double geometricSeries(double a, double r, int n)
{
    return a * (1 - Math.Pow(r, n + 1)) / (1 - r);
}

在其他更复杂的情况下，找到公式可能会更困难。

Answer 2

我知道你的例子是故意的。但是，如果您真正想要计算的仍然是多项式，那么您一定要使用Horner scheme。这是a C# implementation。

Answer 3

你可能正在谈论使用委托进行延期执行。但在许多情况下，它与编写方法相同。例如，让我们从“简单”的方式开始：

public static double SumExponents(double x, int n)
{
    double total = 0;
    for (int i = 1; i <= n; i++)
    {
         total += Math.Pow(x, i);
    }
    return total;
}

这可以使用LINQ编写：

public static double SumExponents(double x, int n)
{
    return Enumerable.Range(1, n)
                     .Select(i => Math.Pow(x, i))
                     .Sum();
}

然后你可以把它写成一个lambda表达式：

Func<double, int, double> func = (x, n) => Enumerable.Range(1, n)
                                              .Select(i => Math.Pow(x, i))
                                              .Sum();

这是你想到的那种事吗？如果没有，请澄清您的问题。你正在寻找什么并不是很明显。

Answer 4

关于geometric progression，C＃没有具体内容。您可以在O（1）时间内计算此总和。（假设电源操作需要恒定的时间。）

在您的情况下，公式将是

x*(x^n - 1)/(x - 1)

Answer 5

int total = 0;
for(int i = 1; i <= n; i++)
    total += Math.Pow(x, i);

Answer 6

除了选择\ sum之外，您还可以使用Aggregate进行折叠序列。

int n;
double x;
double result = Enumerable.Range(1, n)
    .Aggregate(0.0, (acc, i) => acc + Math.Pow(x, i));

如何在C＃中计算这种类型的方程（x ^ 1 + ... x ^ n）？

6 个答案: