Question

我正在尝试在由MCU供电的绘图仪上渲染椭圆，因此可以使用低内存并且优先考虑整数算术。

我有这个等式

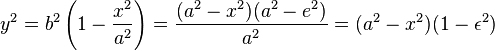
$elipse equation$

我尝试以下列方式在C中实现它：

y = sqrt( (b*b) * ( 1 - ( (x*x) / (a*a) )));

其中y，b，x和a是整数值但结果错误。

Q1这是椭圆方程的正确实现吗？

Q2还有其他方法吗？

Answer 1

是最好的参数方程式。

此处轴对齐椭圆：
```
x=x0+a*cos(t);
y=y0+b*sin(t);
```
其中：
- (x0,y0)是椭圆中心
- a,b是半轴
- t是角度参数t=<0,2*M_PI>
  1. 因此形成一个循环，其中t以一个足够小的步骤
  2. 每个t
  3. 每步的插值/渲染线（从最后一点到新点）
因为x,y,x0,y0,a,b是整数，要么将它们转换为float / double，要么为cos[],sin[]创建整数表，例如：
- int tcos[360],tsin[360];
其中tcos[i]=float(1000.0*cos(float(i)*M_PI/180.0));现在只使用整数，如：
```
for (i=0;i<360;i++)
 {
 x=x0+(a*tcos(i))/1000;
 y=y0+(b*tsin(i))/1000;
 //...
 }
```

如果您需要像素完美渲染或渲染填充椭圆

然后你需要使用不同的方法（与你的等式相同）

使用像素步骤
计算其他轴坐标
渲染两个像素/或填充线

例如轴对齐(0,0)居中椭圆：

for (x=-a;x<=a;x++)
 {
 y = sqrt( (b*b) - ( (x*x*b*b) / (a*a) )));
 // render pixels: (x,+y) and (x,-y) or join them by line
 }

如果你需要整数sqrt，那么实现一个（而不是使用math.h），例如：

int bits(DWORD p)
    {
    DWORD m=0x80000000; int b=32;
    for (;m;m>>=1,b--)
     if (p>=m) break;
    return b;
    }

DWORD sqrt(const DWORD &x)
    {
    DWORD m,a;
    m=(bits(x)>>1); // bits(x) just return position of MSB nonzero bit can use m=16; instead
    if (m) m=1<<m; else m=1;
    for (a=0;m;m>>=1) { a|=m; if (a*a>x) a^=m; }
    return a;
    }

其中DWORD是无符号32位int数据类型。

填写您不需要sqrt

您可以循环浏览该区域并确定该像素是否在内部：

for (y=-b;y<=b;y++)
 for (x=-a;x<=a;x++)
  if ( (y*y) <= ( (b*b) - ( (x*x*b*b) / (a*a) ) ) )
   // render pixel: (x,y)

Answer 2

实施是正确的。我将y，b，x和a设置为double值，这样就修复了错误的输出。

在C中实现椭圆方程的正确方法是什么？

2 个答案: