嵌套for循环中的迭代次数?
所以我从教科书中查看这段代码:
for (int i=0; i<N; i++)
for(int j=i+1; j<N; j++)
作者指出,内部for循环完全迭代N *(N-1)/ 2次,但没有给出他如何达到这样一个等式的基础。我理解N *(N-1),但为什么除以2?我自己运行代码,当N为10时,内部循环迭代45次(10 * 9/2)。
我自己弄乱了代码并尝试了以下内容(仅将i分配给j):
for (int i=0; i<N; i++)
for(int j=i; j<N; j++)
当N = 10时,这导致55.所以我在这里理解基础数学有困难。当然,我可以插入所有的价值观,并通过问题强行解决问题,但我觉得有一些必要的东西,非常简单,我很想念。您如何想出一个用于描述我刚刚构造的for循环的等式?有没有办法在不依赖输出的情况下做到这一点?非常感谢任何帮助,谢谢!
4 个答案:
答案 0 :(得分:10)
考虑每次外循环迭代时会发生什么。第一次是i == 0,因此内部循环从1开始并运行到N-1,这总共是N-1次迭代。下一次通过外循环时,i已增加到1,因此内循环从2开始并一直运行到N-1,总计{{1}迭代。并且该模式继续:第三次通过外循环,您获得N-2次迭代,第四次通过,N-3等。当您到达外循环的最后一次迭代时,{{1因此内部循环以N-4开头并立即停止。所以这是零迭代。
迭代总数是所有这些数字的总和:
i == N-1从另一个角度来看,这只是从j = N到(N-1) + (N-2) + (N-3) + ... + 1 + 0
的正整数之和。这个和的结果称为第(N-1)个三角数,Wikipedia解释了如何找到第n个三角形数的公式为n(n + 1)/ 2。但是在这里你有第(N-1)个三角形数字,所以如果你设置1,你就得到了
N-1答案 1 :(得分:6)
您正在查看嵌套循环,其中外部循环运行N次,内部循环运行(N-1)。你实际上加起来是1 + 2 + 3 + ....
N * (N+1) / 2是数学中的“经典”公式。年轻的卡尔·高斯,后来成为着名的数学家,被给予了课堂上的繁忙工作:将数字从1加到100。老师希望让孩子们忙碌一小时,但卡尔几乎立刻想出了答案:5050。他解释说:1 + 100; 2 + 99; 3 + 98; 4 + 97;等等达到50 + 51.这是50个,每个101。您还可以将其视为(100/2)*(100 + 1);这就是/2的来源。
至于为什么它是(N-1)而不是我提到的(N + 1)...这可能与从1而不是0开始,这会从内循环中删除一次迭代,我认为
答案 2 :(得分:3)
查看内部(j)循环为i的每个值运行多少次。当N = 10时,外(i)循环运行10次,并且j循环应运行0,1,2,3,4,5,6,7,8和9次。现在,您只需将这些数字相加,即可查看内循环运行的次数。您可以使用公式N(N-1)/ 2将0到N-1之间的数字相加。这是adding the numbers from 1 to N众所周知的公式的一个非常小的修改。
对于视觉辅助,您可以看到为什么 1 + 2 + 3 + ... + n = n *(n + 1)/ 2
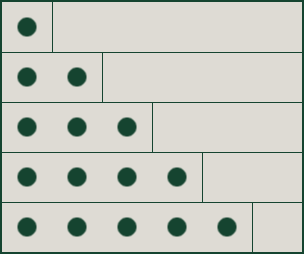
答案 3 :(得分:0)
如果计算内循环的迭代次数,则得到:
1 2 3 4 5 6 7 8 9 10
要获得任意次数迭代的总数,您可以像这样“包装”数字:
0 1 2 3 4
9 8 7 6 5
现在,如果我们添加每个列,则all添加到9(N-1),并且有5(N / 2)列。很明显,对于任何偶数N,我们仍然会得到N / 2列,每列加起来(N-1)。因此,当迭代总数是偶数时,迭代总数总是(N / 2)(N-1),这(由于交换属性)我们可以重写为N (N-1)/ 2。
如果我们在奇数次迭代中做同样的事情,我们就会有一个无法配对的“奇数”列。在这种情况下,我们可以忽略'0',因为我们知道它在任何情况下都不会影响总和。例如,让我们考虑N = 9而不是N = 10。为此,我们得到:
1 2 3 4
8 7 6 5
这给了我们(N-1)/ 2列(9-1 = 8,8 / 2 = 4),每列加起来为N,因此总和将是N *(N-1)/ 2。尽管我们稍微有点不同,但是当N是偶数时,这与上面的公式完全匹配。同样,无论我们使用的列数(即迭代总数)如何,这似乎都是显而易见的。
对于任何N(奇数或偶数),从0到N-1的数字之和为N *(N-1)/ 2.
- 我写了这段代码,但我无法理解我的错误
- 我无法从一个代码实例的列表中删除 None 值,但我可以在另一个实例中。为什么它适用于一个细分市场而不适用于另一个细分市场?
- 是否有可能使 loadstring 不可能等于打印?卢阿
- java中的random.expovariate()
- Appscript 通过会议在 Google 日历中发送电子邮件和创建活动
- 为什么我的 Onclick 箭头功能在 React 中不起作用?
- 在此代码中是否有使用“this”的替代方法?
- 在 SQL Server 和 PostgreSQL 上查询,我如何从第一个表获得第二个表的可视化
- 每千个数字得到
- 更新了城市边界 KML 文件的来源?