Question

从n维单位单形中随机均匀采样是一种奇特的方式，可以说你需要n个随机数，这样

他们都是非负面的，
他们总结为一个，
总和为1的n个非负数的每个可能向量都是相同的。

在n = 2的情况下，您希望从正象限中的线x + y = 1（即y = 1-x）的线段均匀采样。在n = 3的情况下，你是从平面的三角形部分采样x + y + z = 1，它位于R3的正八分圆中：

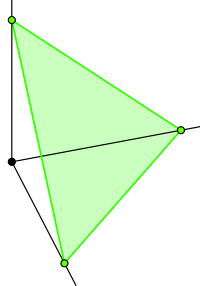
（来自http://en.wikipedia.org/wiki/Simplex的图片。）

请注意，选择n个统一的随机数，然后将它们归一化，使它们总和为1则不起作用。你最终会偏向不那么极端的数字。

同样地，选择n-1个均匀随机数然后将第n个减去它们的总和也会引入偏差。

维基百科提供了两种算法来正确执行此操作：http://en.wikipedia.org/wiki/Simplex#Random_sampling （虽然第二个目前声称只是在实践中是正确的，而不是在理论上。我希望在我理解这一点时清理它或澄清它。我最初陷入了“警告：这样的论文声称以下是错误的“在维基百科页面上，其他人把它变成了”只在实践中工作“的警告。）

最后，问题是：你认为Mathematica中单纯形采样的最佳实现是什么（最好用经验证实它是正确的）？

相关问题

Answer 1

此代码可以工作：

samples[n_] := Differences[Join[{0}, Sort[RandomReal[Range[0, 1], n - 1]], {1}]]

基本上，您只需在n - 1间隔选择[0,1]个地点即可将其拆分，然后使用Differences获取每个部分的大小。

快速运行Timing表明它比Janus的第一个答案快一点。

Answer 2

经过一番挖掘，我发现this page给出了Dirichlet分布的一个很好的实现。从那里看来，遵循维基百科的方法1似乎很简单。这似乎是最好的方法。

作为测试：

In[14]:= RandomReal[DirichletDistribution[{1,1}],WorkingPrecision->25]
Out[14]= {0.8428995243540368880268079,0.1571004756459631119731921}
In[15]:= Total[%]
Out[15]= 1.000000000000000000000000

100个样本的图：

alt text http://www.public.iastate.edu/~zdavkeos/simplex-sample.png

Answer 3

我使用zdav：Dirichlet分布似乎是最简单的方法，zdav引用的Dirichlet分布的采样算法也出现在Dirichlet distribution的维基百科页面上。

实施方式，首先进行完整的Dirichlet分布需要一些开销，因为你真正需要的是n个随机Gamma[1,1]个样本。比较下面
简单实施

SimplexSample[n_, opts:OptionsPattern[RandomReal]] :=
  (#/Total[#])& @ RandomReal[GammaDistribution[1,1],n,opts]

完整Dirichlet实施

DirichletDistribution/:Random`DistributionVector[
 DirichletDistribution[alpha_?(VectorQ[#,Positive]&)],n_Integer,prec_?Positive]:=
    Block[{gammas}, gammas = 
        Map[RandomReal[GammaDistribution[#,1],n,WorkingPrecision->prec]&,alpha];
      Transpose[gammas]/Total[gammas]]

SimplexSample2[n_, opts:OptionsPattern[RandomReal]] := 
  (#/Total[#])& @ RandomReal[DirichletDistribution[ConstantArray[1,{n}]],opts]

<强>时序

Timing[Table[SimplexSample[10,WorkingPrecision-> 20],{10000}];]
Timing[Table[SimplexSample2[10,WorkingPrecision-> 20],{10000}];]
Out[159]= {1.30249,Null}
Out[160]= {3.52216,Null}

因此完整的Dirichlet慢了3倍。如果您一次需要m> 1个样本点，那么您可以通过(#/Total[#]&)/@RandomReal[GammaDistribution[1,1],{m,n}]进一步获胜。

Answer 4

这是来自Wikipedia的第二个算法的简洁实现：

SimplexSample[n_] := Rest@# - Most@# &[Sort@Join[{0,1}, RandomReal[{0,1}, n-1]]]

这是从这里改编的：http://www.mofeel.net/1164-comp-soft-sys-math-mathematica/14968.aspx （最初它有联盟而不是排序@加入 - 后者稍微快一些。）

（有关证据证明这是正确的，请参阅评论！）

Answer 5

我已经创建了一种在单纯形上均匀随机生成的算法。您可以在以下链接中找到论文中的详细信息： http://www.tandfonline.com/doi/abs/10.1080/03610918.2010.551012#.U5q7inJdVNY

简单来说，您可以使用以下递归公式来查找n维单形上的随机点：

X 的<子> 1 = 1 - - [R 的<子> 1 ^{1 / N-1}

X 的<子>的ķ的 =（1-Σ<子> I = 1 ^的ķ的 X 的<子>的 I 的）（1- - [R 的<子>的ķ ^{1 / nk}），k = 2，...，n-1

X 的<子> 名词的 = 1-Σ<子> I = 1 ^N-1 X 的<子>的 I 的

其中R_i是0到1之间的随机数。

现在我正在尝试制作一个算法，从受约束的单纯形中生成随机均匀样本。这是单纯形和凸形体之间的交叉。

从n维单位单形中随机均匀地采样

5 个答案: