如何在matlab中分析矢量外积

Question

在我的matlab分析期间，我注意到一行代码消耗的时间比我想象的多得多。知道如何让它更快吗？

X = Y(ids_A, ids_A) - (Y(ids_A,k) * Y(k,ids_A))/Y(k,k); 

X和Y是具有相同大小（dxd）的对称矩阵，k是Y中单个行/列的索引，ids_A是所有其他行/列的索引向量（因此Y（ids_A， k）是列向量，Y（k，ids_A）是行向量）

ids_A = setxor(1:d,k); 

谢谢！

Answer 1

您可以通过调用bsxfun来替换外部产品乘法：

X = Y(ids_A, ids_A) - (bsxfun(@times, Y(ids_A,k), Y(k,ids_A))/Y(k,k));

那么上面的代码是如何工作的呢？让我们看一下当一个向量是4个元素而另外3个元素时外部产品的定义：

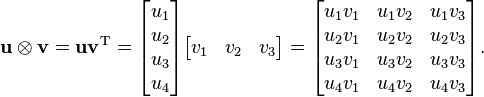
^{来源：Wikipedia}

如您所见，外部产品由元素产品创建，其中第一个向量u水平复制，而第二个向量v垂直复制。然后，您可以找到每个元素的元素产品，以生成结果。这是用bsxfun：

雄辩地完成的

bsxfun(@times, u, v.');

u将是列向量，v.'将是行向量。 bsxfun自然地复制数据以遵循上述模式，然后我们使用@times来执行元素方面的产品。

Answer 2

我假设您的代码看起来像这样 -

for k = 1:d
    ids_A = setxor(1:d,k);
    X = Y(ids_A, ids_A) - (Y(ids_A,k) * Y(k,ids_A))/Y(k,k);
end

使用给定的代码段，可以安全地假设您在该循环中以某种方式使用X。您可以在开始此循环之前计算所有X矩阵作为预计算步骤，这些计算可以作为矢量化方法执行。

关于代码片段本身，可以看出你正在逃避＆＃34;逃避＆＃34;每次迭代时使用setxor的一个索引。现在，如果您使用矢量化方法，您可以在 one-go 中执行所有这些数学运算，然后删除在矢量化方法中合并的元素，但不是预期的。这确实是下一个列出的基于 bsxfun 的矢量化方法的精髓 -

%// Perform all matrix-multiplications in one go with bsxfun and permute
mults = bsxfun(@times,permute(Y,[1 3 2]),permute(Y,[3 2 1]));

%// Scale those with diagonal elements from Y and get X for every iteration
scaledvals = bsxfun(@rdivide,mults,permute(Y(1:d+1:end),[1 3 2]));
X_vectorized = bsxfun(@minus,Y,scaledvals);

%// Find row and column indices as linear indices to be removed from X_all
row_idx = bsxfun(@plus,[0:d-1]*d+1,[0:d-1]'*(d*d+1));
col_idx = bsxfun(@plus,[1:d]',[0:d-1]*(d*(d+1)));

%// Remove those "setxored" indices and then reshape to expected size
X_vectorized([row_idx col_idx])=[];
X_vectorized = reshape(X_vectorized,d-1,d-1,d);

基准

基准代码

d = 50;          %// Datasize
Y = rand(d,d);    %// Create random input
num_iter = 100;   %// Number of iterations to be run for each approach

%// Warm up tic/toc.
for k = 1:100000
    tic(); elapsed = toc();
end

disp('------------------------------ With original loopy approach')
tic
for iter = 1:num_iter
    for k = 1:d
        ids_A = setxor(1:d,k);
        X = Y(ids_A, ids_A) - (Y(ids_A,k) * Y(k,ids_A))/Y(k,k);
    end
end
toc
clear X k ids_A

disp('------------------------------ With proposed vectorized approach')
tic
for iter = 1:num_iter
    mults = bsxfun(@times,permute(Y,[1 3 2]),permute(Y,[3 2 1]));
    scaledvals = bsxfun(@rdivide,mults,permute(Y(1:d+1:end),[1 3 2]));
    X_vectorized = bsxfun(@minus,Y,scaledvals);

    row_idx = bsxfun(@plus,[0:d-1]*d+1,[0:d-1]'*(d*d+1));
    col_idx = bsxfun(@plus,[1:d]',[0:d-1]*(d*(d+1)));

    X_vectorized([row_idx col_idx])=[];
    X_vectorized = reshape(X_vectorized,d-1,d-1,d);
end
toc

<强>结果

案例＃1：d = 50

------------------------------ With original loopy approach
Elapsed time is 0.849518 seconds.
------------------------------ With proposed vectorized approach
Elapsed time is 0.154395 seconds.

案例＃2：d = 100

------------------------------ With original loopy approach
Elapsed time is 2.079886 seconds.
------------------------------ With proposed vectorized approach
Elapsed time is 2.285884 seconds.

案例＃1：d = 200

------------------------------ With original loopy approach
Elapsed time is 7.592865 seconds.
------------------------------ With proposed vectorized approach
Elapsed time is 19.012421 seconds.

<强>结论

人们可以很容易地注意到，在处理大小超过100 x 100的矩阵时，所提出的向量化方法可能是更好的选择。 内存饥渴的bsxfun 让我们失望。