如何总结序列?
我如何总结以下顺序:
⌊n/1⌋ + ⌊n/2⌋ + ⌊n/3⌋ + ... + ⌊n/n⌋
这只是C ++上的O(n)解决方案:
#include <iostream>
int main()
{
int n;
std::cin>>n;
unsigned long long res=0;
for (int i=1;i<=n;i++)
{
res+= n/i;
}
std::cout<<res<<std::endl;
return 0;
}
你知道比这更好的解决方案吗?我的意思是O(1)或O(log(n))。感谢您的时间:)和解决方案
编辑: 谢谢你的所有答案。如果有人想要解决方案O(sqrt(n)): 的Python:
import math
def seq_sum(n):
sqrtn = int(math.sqrt(n))
return sum(n // k for k in range(1, sqrtn + 1)) * 2 - sqrtn ** 2
n = int(input())
print(seq_sum(n))
C ++:
#include <iostream>
#include <cmath>
int main()
{
int n;
std::cin>>n;
int sqrtn = (int)(std::sqrt(n));
long long res2 = 0;
for (int i=1;i<=sqrtn;i++)
{
res2 +=2*(n/i);
}
res2 -= sqrtn*sqrtn;
std::cout<<res2<<std::endl;
return 0;
}
5 个答案:
答案 0 :(得分:24)
这是Dirichlet's divisor summatory function D(x)。使用以下公式(source)

,其中

给出了以下O(sqrt(n))伪代码(碰巧是有效的Python):
def seq_sum(n):
sqrtn = int(math.sqrt(n))
return sum(n // k for k in range(1, sqrtn + 1)) * 2 - sqrtn ** 2
注意:
- Python中的
//运算符是整数,即截断,除法。 -
math.sqrt()用作说明。严格地说,这应该使用exact integer square root algorithm而不是浮点数学。
答案 1 :(得分:7)
答案 2 :(得分:5)
Polymath项目描绘了一个在时间O(n ^(1/3 + o(1)))中计算此函数的算法,请参阅第8-9页的第2.1节:
http://arxiv.org/abs/1009.3956
该算法包括将区域切割成足够薄的区间,并估计每个区域的值,其中区间选择为足够薄,以便在舍入到最接近的整数时估计将是精确的。所以你直接计算到某个范围(他们建议100n ^(1/3),但你可以小心地修改它)然后在这些薄片中做其余的。
有关此序列的详细信息,请参阅the OEIS entry。
编辑:我现在看到Kerrek SB在评论中提到了这个算法。然而,公平地说,我在5年前向OEIS添加了评论,所以我对发布“他的”答案感到不舒服。 :)
我还应该提到没有O(1)算法是可能的,因为答案是在n log n附近,因此即使写出也需要时间&gt; log n。
答案 3 :(得分:1)
我们将所有数字{1, 2, 3, ..., n}分成两组:小于或等于sqrt(n)且大于sqrt(n)。对于第一组,我们可以通过简单迭代计算总和。对于第二组,我们可以使用以下观察:a > sqrt(n),而不是n / a < sqrt(n)。这就是我们可以迭代[n / i] = d(从1到sqrt(n))的值并计算i的{{1}}的数量的原因。使用[n / i] = d表示O(1)的事实d可以在[n / i] = d中找到固定i * d <= n and i * (d + 1) > n的{{1}}。
第一组和第二组在[n / (d + 1)] < i <= [n / d]处理,共计O(sqrt(n))次。
答案 4 :(得分:0)
- 我写了这段代码,但我无法理解我的错误
- 我无法从一个代码实例的列表中删除 None 值,但我可以在另一个实例中。为什么它适用于一个细分市场而不适用于另一个细分市场?
- 是否有可能使 loadstring 不可能等于打印?卢阿
- java中的random.expovariate()
- Appscript 通过会议在 Google 日历中发送电子邮件和创建活动
- 为什么我的 Onclick 箭头功能在 React 中不起作用?
- 在此代码中是否有使用“this”的替代方法?
- 在 SQL Server 和 PostgreSQL 上查询,我如何从第一个表获得第二个表的可视化
- 每千个数字得到
- 更新了城市边界 KML 文件的来源?

 时间解决方案。
时间解决方案。 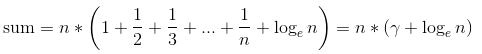
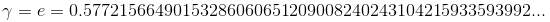
 是一个超越数字。)
是一个超越数字。)