如何在MATLAB中绘制显示2D高斯函数总和的图像？

Question

我需要在同一个2D域中生成两个高斯函数，然后在两个域上总结这两个函数的值，以生成高斯混合。在图像中的所有像素位置，我们需要两个高斯函数的和，这将给出全局分布的良好近似。

我怎么能在MATLAB中做到这一点？

Answer 1

使用meshgrid很容易实现。您需要生成一组X和Y点，然后将这些点用作具有已知方法和标准差的两个高斯函数的输入。完成此操作后，您只需将它们相加，然后就可以使用mesh将其可视化。回想一下2D高斯的定义：

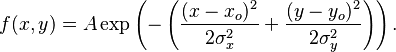
^{来源：Wikipedia}

---

小注：参考这篇文章的评论，Amro做了一个很好的观察，我们假设给定分布的协方差矩阵是对角线的。这意味着您的数据的每个维度不会彼此共同变化并且是独立的。如果情况不是这样，那么这将需要更复杂的计算，但可以使用矩阵运算轻松实现：https://en.wikipedia.org/wiki/Multivariate_normal_distribution#Density_function。由于您还没有真正向我提供有关数据分布的任何信息，我将假设每个维度不会共变，并且您有一个对角线协方差矩阵。如果你想看到关于如何绘制2D高斯混合物的更详细和更一般的案例，你也可以在这里查看他的帖子：https://stackoverflow.com/a/26070081/97160

---

x_0和y_0是x和y方向的平均值，而o_x和o_y表示x中的标准偏差{1}}和y方向。 A是一个归一化常数，为简单起见，通常为1。您只需要生成一个跨越某些已知维度的坐标网格，然后指定2对均值和标准偏差，为每个参数运行此表达式，然后在添加两个参数后显示结果。我们假设网格跨越-10 <= (x,y) <= 10。另外，假设我的平均值和标准偏差如下：

x_1 = 2
x_2 = 2
y_1 = -1
y_2 = -1

o_x_1 = 1
o_y_1 = 2
o_x_2 = 2
o_y_2 = 1

因此，x_1, y_1是第一高斯的x和y方向的均值，x_2, y_2是第二高斯的均值，o_x_1, o_y_1是x和y方向上第一个高斯的标准偏差，o_x_2, o_y_2是x和y中第二个高斯的标准偏差方向。因此，您的代码实际上只需要执行此操作：

%// Define grid of points
[X,Y] = meshgrid(-10:0.01:10, -10:0.01:10);

%// Define parameters for each Gaussian
x_1 = 2;
y_1 = 2;
x_2 = -1;
y_2 = -1;

o_x_1 = 1;
o_y_1 = 2;
o_x_2 = 2;
o_y_2 = 1;

%// Define constant A... let's just assume 1 for both
A = 1;

%// Generate Gaussian values for both Gaussians
f1 = A*exp( -( ((X - x_1).^2 / (2*o_x_1^2)) + ((Y - y_1).^2 / (2*o_y_1^2)) ) );
f2 = A*exp( -( ((X - x_2).^2 / (2*o_x_2^2)) + ((Y - y_2).^2 / (2*o_y_2^2)) ) );

%// Add them up
f = f1 + f2;

%// Show the results
mesh(X, Y, f);
%// Label the axes
xlabel('x');
ylabel('y');
zlabel('z');
view(-130,50); %// For a better view
colorbar; %// Add a colour bar for good measure

这是我得到的情节，一旦我调整观察相机以获得更好的视角，并在图的右侧显示一个颜色条，以说明情节高度的直观表示。

要了解这两者是如何混合的，让我们将相机直接指向上方。您可以通过以下方式调整视角以将摄像机直接移动到绘图上方：

view(0, 90);

这就是我得到的：

根据上图，我们正在做的事情更为明显。你可以看到高斯人居中的位置。具体而言，第一高斯为(x,y) = (2,2)，第二高斯为(x,y) = (-1,-1)。

你也可以看到它们合并，因为每个高斯上都有尾巴最终相互接触，当你加起来时，你会看到这种合并效果。而且，高斯人的一般形状是我们所期望的。对于以(x,y) = (2,2)为中心的第一个，我将水平标准差设为1而垂直标准偏差为2，因此相对于y方向自然会更高。类似地，对于以(x,y) = (-1,-1)为中心的第二个，我翻转了标准偏差，因此我们希望这相对于x方向更宽。

这是你可以开始的事情。我真的不知道你的最终应用程序是什么，但也许这段代码可以帮助你。鉴于您的问题描述，我尽了最大努力。

玩得开心！