如何计算单个点质量？

Question

我正在研究C＃2d软体物理引擎，我需要将质量分配给给定的对象顶点：顶点列表（x，y位置），对象的总质量和质心。

质心如下：

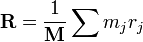
其中，

R = center of mass
M = total mass
mj = mass of vertex j
rj = position of vertex j

我需要一种能够近似给定R，M和rj的每个mj的算法。

编辑我只想澄清一点，我知道有一套无限的解决方案。我正在寻找一个快速算法，找到一组mj（这样它们都足够接近mj = M / [顶点数]，并且“充分”被定义为一些小的浮点阈值）。

此外，每个对象将包含大约5到35个点。

Answer 1

您可以按如下方式计算均匀密集多边形的CM：从0..N-1中对N个顶点进行编号，并循环处理它们，以便顶点N包裹到顶点0：

total_area = sum[i=0..N-1]( X(p[i],p[i+1])/2 )
CM = sum[i=0..N-1]( (p[i]+p[i+1])*X(p[i],p[i+1])/6 ) / total_area

   where X(p,q)= p.x*q.y - q.x*p.y  [basically, a 2D cross product]

如果多边形是凸面，则CM将位于多边形内部，因此您可以合理地开始通过切割三角形中的区域（如饼图），并将CM放在中心处。您应该能够使用其质量的三分之一对三角形的每个顶点进行加权，而不更改CM - 但是，这仍然会使整个多边形的CM的总质量的三分之一。尽管如此，将质量传递缩放3/2应该可以分割两个“外部”顶点之间每个三角形的质量。结果，

area[i] = X( (p[i]-CM), (p[i+1]-CM) ) / 2
   (this is the area of the triangle between the CM and vertices i and i+1)

mass[i] = (total_mass/total_area) * (area[i-1] + area[i])/2

请注意，这种传质是非常“非物质的” - 如果没有别的，如果按照字面意思对待，它会使惯性的瞬间变得凶狠。但是，如果你需要在顶点之间分配质量（比如某种俗气的爆炸），并且你不想在这样做时破坏CM，这应该可以解决问题。

最后，有几个警告：

• 如果你不使用实际的CM，它将无法正常工作
• 在凹形物体上使用它是危险的;你最终会面临消极群众的风险

Answer 2

计算自由度：对于D维空间中的点，D+1方程[+]和n未知数为n个单独的粒子。如果n>D+1你沉没了（除非你得到的信息比你告诉我们的更多：对称约束，高阶矩等......）。

编辑：我的早期版本假设你有m_i并正在寻找r_i。如果您拥有r_i并想要m_i s。

，情况会稍好一些

[+] _{上面列出的那个（实际D单独的等式）和M = \sum m_j}

---

Arriu说：

  对不起，我误解了你的问题。我以为你在问我是不是在设计诸如圆环，圆环或戒指等物体（带有镂空的物体......）。我只用外壳（如气球或气泡）塑造身体。我不需要比这更复杂的东西。

现在我们到了某个地方。你做了解更多。

您可以通过将对象的表面区域划分为相邻点之间的三角形来近似。该总面积为您提供平均质量密度。现在找到DoF缺陷，并根据平均密度和它所参与的每个三角形的面积的1/3，分配许多r_i s（随机抽取，我猜）。然后分析解决剩余的系统。如果问题是病态的，您可以绘制一组新的指定点，或者尝试随机游走您已经猜到的质量。

Answer 3

随着顶点移动，质心R将不断变化。因此，如果您有10个顶点，则存储10个连续“帧”的值 - 这将为您的10个未知数提供10个方程式（假设质量不随时间变化）。

Answer 4

我会解决问题。也就是说，给定一个密度和物体的位置（当然它自然仍然是物体的质心和三个矢量对应于物体的方向，参见欧拉的角度），在每个顶点将一个体积与该物体相关联。元素（它将随分辨率而变化，对于对象边缘的位置可能是分数），并将密度（d_j）与相关的体积（v_j），m_j = v_j * d_j相乘。这种方法应该能够自然地再现物体质量的中心。

也许我不理解你的问题，但考虑到这最终会产生正确的质量（质量=总和（m_j）=总和（v_j * d_j）），最坏的情况是这种方法应该得出你的结果的验证。