Aµś¤Õ«×µ¢Į’╝īµ▓Īµ£ēµēŠÕł░µ£Ćń¤ŁĶĘ»ÕŠäķŚ«ķóś
µłæµ£ēõ╗ŻńĀüÕÅ»õ╗źµēŠÕł░õ╗ÄAńé╣Õł░Bńé╣ńÜäµ£Ćń¤ŁĶĘ»ÕŠäŃĆéõĖ║µŁż’╝īµłæõĮ┐ńö©ńÜ䵜»Aµś¤ÕÅśÕī¢ŃĆ鵳æõĮ┐ńö©õ║īń╗┤µĢ░ń╗äµØźĶĪ©ńż║õĖĆõĖ¬õ║īń╗┤ńĮæµĀ╝’╝īõĮåµłæńÜäĶĘ»ÕŠäõĖŹķććńö©Õ»╣Ķ¦Æń║┐Õ┐½µŹĘµ¢╣Õ╝Å’╝īÕŬµ£ēÕĘ”’╝īÕÅ│’╝īõĖŖÕÆīõĖŗŃĆéÕł░ńø«ÕēŹõĖ║µŁóõĖĆÕłćµŁŻÕĖĖ’╝īõĮåÕ«āÕ╣ČõĖŹµĆ╗ĶāĮµēŠÕł░µ£Ćń¤ŁńÜäĶĘ»ÕŠäŃĆ鵳æµā│ń¤źķüōÕć║õ║åõ╗Ćõ╣łķŚ«ķóś’╝īõĖ║õ╗Ćõ╣łõ╝ÜÕć║ķöÖ’╝īõ╗źÕÅŖÕ”éõĮĢĶ¦ŻÕå│Õ«āŃĆéµÅÉÕēŹĶ░óĶ░óŃĆé
Ķ┐Öµś»õĖĆÕ╝ĀÕøŠńēćµØźĶ»┤µśÄń®Čń½¤ÕÅæńö¤õ║åõ╗Ćõ╣ł’╝Ü
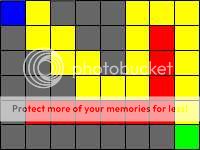
Ķ┐Öµś»µłæńÜäõ╗ŻńĀü’╝łĶĘ»ÕŠäµ¤źµēŠń▒╗ķ”¢Õģł’╝īńäČÕÉĵś»Õ«āńÜäÕŖ®µēŗń▒╗’╝ē’╝Ü
BTW’╝ܵĢ░ÕŁ”ÕÉæķćÅÕŬõĖŹĶ┐浜»õĖĆõĖ¬ÕćĀõĮĢńé╣ń▒╗’╝īĶĆīõĖöplayerTileLocationÕÆīenemyTileLocationķāĮÕŬµś»õĖÄńĮæµĀ╝õĖŖńÜäĶĄĘÕ¦ŗĶŖéńé╣ÕÆīń╗ōµØ¤ĶŖéńé╣ńøĖÕ»╣Õ║öńÜäńé╣ŃĆéÕÅ”Õż¢’╝īµłæõĮ┐ńö©AStarNodeń▒╗õĮ£õĖ║Õ£░ÕøŠõĖŖµēƵ£ēÕøŠÕØŚńÜäĶŖéńé╣’╝īĶĆīõĖŹµś»ÕĖĖĶ¦äÕ»╣Ķ▒ĪŃĆépackage {
import src.Characters.Character;
import src.InGame.Map;
import src.Maths.MathVector;
public final class BaseAI {
// REPRESENTS UP, DOWN, RIGHT, AND LEFT OF ANY ONE NODE
private static const bordersOfNode:Array = new Array(
new MathVector( -1, 0), new MathVector(1, 0), new MathVector(0, -1), new MathVector(0, 1));
private var _player:Character;
private var map:Map;
private var playerTileLocation:MathVector;
private var openList:Array;
private var closedList:Array;
// 2D ARRAY OF MAP TILES (I DON'T USE HERE, BUT I PLAN TO IN FUTURE)
private var mapArray:Array;
private var originNode:AStarNode;
private var complete:Boolean;
public function BaseAI(_player:Character,map:Map):void {
this._player = _player;
this.map = map;
openList = new Array();
closedList = new Array();
mapArray = map.tiles;
}
public function get player():Character {
return this._player;
}
public function calculatePlayerTileLocation():void {
playerTileLocation = map.worldToTilePoint(player.groundPosition);
}
//WILL EVENTUAL RETURN A DIRECTION FOR THE ENEMY TO TAKE THAT ITERATION (EVERY 1-2 SECONDS)
public function getDirection(enemy:Character):String {
var enemyTileLocation:MathVector = map.worldToTilePoint(enemy.groundPosition);
originNode = new AStarNode(enemyTileLocation, playerTileLocation);
originNode.setAsOrigin();
openList = [originNode];
closedList = [];
complete = false;
var currentNode:AStarNode;
var examiningNode:AStarNode;
while (!complete) {
openList.sortOn("F", Array.NUMERIC);
currentNode = openList[0];
closedList.push(currentNode);
openList.splice(0, 1);
for (var i in bordersOfNode) {
examiningNode = new AStarNode(new MathVector(currentNode.X + bordersOfNode[i].x, currentNode.Y + bordersOfNode[i].y),playerTileLocation);
if (map.isOpenTile(map.getTile(examiningNode.X, examiningNode.Y)) && !examiningNode.isThisInArray(closedList)) {
if (!examiningNode.isThisInArray(openList)) {
openList.push(examiningNode);
examiningNode.parentNode = currentNode;
}else {
}
if (examiningNode.X == playerTileLocation.x && examiningNode.Y == playerTileLocation.y) {
complete = true;
var done:Boolean = false;
var thisNode:AStarNode;
thisNode = examiningNode;
while (!done) {
if (thisNode.checkIfOrigin()) {
done = true;
}else {
thisNode = thisNode.parentNode;
}
}
}
}
}
}
}
}
}
package {
import src.Maths.MathVector;
internal final class AStarNode {
private var _X:int;
private var _Y:int;
private var _G:int;
private var _H:int;
private var _F:int;
private var _parentNode:AStarNode;
private var _isOrigin:Boolean;
public static const VERTICAL:uint = 10;
public function AStarNode(thisNodeLocation:MathVector, targetNodeLocation:MathVector) {
X = thisNodeLocation.x;
Y = thisNodeLocation.y;
H = Math.abs(X - targetNodeLocation.x) + Math.abs(Y - targetNodeLocation.y);
G = 0;
F = H + G;
}
public function set X(newX:int):void {
this._X = newX;
}
public function get X():int {
return this._X;
}
public function set Y(newY:int):void {
this._Y = newY;
}
public function get Y():int {
return this._Y;
}
public function set G(newG:int):void {
this._G = newG;
}
public function get G():int {
return this._G;
}
public function set H(newH:int):void {
this._H = newH;
}
public function get H():int {
return this._H;
}
public function set F(newF:int):void {
this._F = newF;
}
public function get F():int {
return this._F;
}
public function set parentNode(newParentNode:AStarNode):void {
this._parentNode = newParentNode;
}
public function get parentNode():AStarNode {
return this._parentNode;
}
public function setAsOrigin():void {
_isOrigin = true;
}
public function checkIfOrigin():Boolean {
return _isOrigin;
}
public function isThisInArray(arrayToCheck:Array):Boolean {
for (var i in arrayToCheck) {
if (arrayToCheck[i].X == this.X && arrayToCheck[i].Y == this.Y) {
return true
}
}
return false
}
}
enter code here
}
2 õĖ¬ńŁöµĪł:
ńŁöµĪł 0 :(ÕŠŚÕłå’╝Ü1)
Õ┐½ķƤµĄÅĶ¦łõĖĆõĖŗõ╗ŻńĀüõ╝ܵÅÉÕć║ķöÖĶ»»ÕÉ»ÕÅæÕ╝ÅńÜäµā│µ│ĢŃĆéµé©ńÜäGÕĆ╝Õ£©ĶŖéńé╣õĖŁÕ¦ŗń╗łõĖ║0’╝īĶć│Õ░æµłæń£ŗõĖŹÕł░Õ«āÕÅ»õ╗źµø┤µö╣ńÜäõĮŹńĮ«ŃĆéõĮåµś»’╝īÕ£©A-starń«Śµ│ĢõĖŁ’╝īµé©ńÜäõ╗╗ÕŖĪ’╝łµēŠÕł░µ£ēķÜ£ńóŹńē®ńÜäµ£Ćń¤ŁĶĘ»ÕŠä’╝ēÕ║öĶ»źõ╗ŻĶĪ©ÕĘ▓ń╗ÅÕł░ĶŠŠÕ░ÅÕī║ńÜ䵣źµĢ░ŃĆéĶ┐ÖÕ░åÕģüĶ«Ėń«Śµ│Ģńö©ĶŠāń¤ŁńÜäĶĘ»ÕŠäµø┐µŹóķĢ┐ĶĘ»ÕŠäŃĆé
ńŁöµĪł 1 :(ÕŠŚÕłå’╝Ü0)
µ£ēõĖƵ¼Īµłæń╝¢ÕåÖõ║åõĖĆõĖ¬Aµś¤'ń«Śµ│Ģ'’╝īµłæõĮ┐ńö©õ║åõĖĆõĖ¬õ║īń╗┤µĢ░ń╗äõĮ£õĖ║ńĮæµĀ╝’╝łÕ░▒ÕāÅõĮĀõĖƵĀĘ’╝ēŃĆéÕ£©µÉ£ń┤óÕ╝ĆÕ¦ŗµŚČ’╝īµ»ÅõĖ¬ńĮæµĀ╝õĮŹńĮ«ńÜäŌĆ£µÉ£ń┤óŌĆØÕ▒׵ƦķāĮĶ«ŠńĮ«õĖ║falseŃĆéµ»ÅõĖ¬ńĮæµĀ╝õĮŹńĮ«õ╣¤µ£ēõĖĆõĖ¬Ķ┐׵ğµ¢╣ÕÉæķśĄÕłŚ;ńĮիČÕÅ»õ╗źķĆēµŗ®Ķ┐øÕģźńÜäķĆēķĪ╣ - µ£ēõ║øÕÅ»ĶāĮµś»Õ╝ƵöŠńÜä’╝īµ£ēõ║øÕÅ»ĶāĮĶó½Õ░üķöüõĖöµŚĀµ│ĢĶ«┐ķŚ« µłæõ╝ÜķĆÜĶ┐浯Ƶ¤źĶĄĘÕ¦ŗńĮæµĀ╝õĮŹńĮ«µØźµ¤źń£ŗÕ«āµ£ēÕżÜÕ░æµ¢╣ÕÉæķĆēķĪ╣µØźÕ╝ĆÕ¦ŗµÉ£ń┤óŃĆéÕ»╣õ║ĵ»ÅõĖ¬ķĆēķĪ╣’╝īµłæõ╝ÜÕ░å'path'µĢ░ń╗äµÄ©Õģź_pathsµĢ░ń╗äŃĆéµ»ÅõĖ¬'path'µĢ░ń╗äµ£Ćń╗łķāĮõ╝ÜÕīģÕɽõĖĆń│╗ÕłŚ'move'’╝ł0ĶĪ©ńż║up’╝ī1ĶĪ©ńż║right’╝ī2ĶĪ©ńż║down’╝ī3ĶĪ©ńż║left’╝ēŃĆéÕøĀµŁż’╝īÕ»╣õ║ĵ»ÅõĖ¬ÕłØÕ¦ŗĶĘ»ÕŠä’╝īµłæõ╝ܵĩĶ┐øńøĖÕ║öńÜäÕ╝ĆÕ¦ŗń¦╗ÕŖ©ŃĆ鵳æĶ┐śÕ░åńĮæµĀ╝õĮŹńĮ«ńÜäŌĆ£µÉ£ń┤óŌĆØÕ▒׵ƦĶ«ŠńĮ«õĖ║true ńäČÕÉĵłæõ╝ÜķüŹÕÄ嵻ŵØĪĶĘ»ÕŠä’╝īĶ┐ÉĶĪīĶ┐ÖõĖĆń│╗ÕłŚńÜäń¦╗ÕŖ©õ╗źÕł░ĶŠŠµ£ĆĶ┐æµĘ╗ÕŖĀńÜäõĮŹńĮ«ŃĆ鵳æõ╝ܵŻĆµ¤źĶ»źõĮŹńĮ«µś»ÕÉ”µś»ńø«µĀćõĮŹńĮ«ŃĆéÕ”éµ×£õĖŹµś»’╝īµłæõ╝ÜÕ░åĶ»źõĮŹńĮ«µĀćĶ«░õĖ║ÕĘ▓µÉ£ń┤ó’╝īńäČÕÉĵŻĆµ¤źÕÅ»ńö©ńÜäµ¢╣ÕÉæ’╝īÕ┐ĮńĢźÕĘ▓µÉ£ń┤óĶ┐ćńÜäõĮŹńĮ«ŃĆéÕ”éµ×£ķØ×ÕÅ»ńö©’╝īÕłÖĶĘ»ÕŠäÕ░åĶó½Õģ│ķŚŁÕ╣Čõ╗ÄĶĘ»ÕŠäµĢ░ń╗äõĖŁŌĆ£µŗ╝µÄźŌĆØ ÕÉ”ÕłÖ’╝īõĖ║µ»ÅõĖ¬ÕÅ»ńö©ńÜäń¦╗ÕŖ©ķĆēķĪ╣ÕłČõĮ£ÕĮōÕēŹĶĘ»ÕŠäµĢ░ń╗äńÜäByteArrayŌĆ£µĘ▒µŗĘĶ┤ØŌĆØ’╝īĶČģĶ┐ćń¼¼õĖĆõĖ¬ń¦╗ÕŖ©ķĆēķĪ╣ŃĆéÕ£©õĖĆõĖ¬µ¢╣ÕÉæõĖŖńÜäń¦╗ÕŖ©Ķó½µĘ╗ÕŖĀÕł░ÕĮōÕēŹĶĘ»ÕŠäÕÆīµ¢░ĶĘ»ÕŠäõĖŁ’╝īÕ£©Õ«āõ╗¼ÕÉäĶć¬ńÜäµ¢╣ÕÉæõĖŖ Õ”éµ×£ĶĘ»ÕŠäµĢ░ĶŠŠÕł░0’╝īÕłÖõĖżõĖ¬õĮŹńĮ«õ╣ŗķŚ┤µ▓Īµ£ēĶĘ»ÕŠäŃĆé µłæĶ«żõĖ║Ķ┐Öµś»Õģ│õ║ÄÕ«āńÜäŃĆ鵳æÕĖīµ£øĶ┐ÖÕ»╣õĮĀµ£ēµēĆÕĖ«ÕŖ® Ķ»Ęµ│©µäÅ’╝īµÉ£ń┤óõĖŹķ£ĆĶ”üŌĆ£Õ«ÜÕÉæŌĆØÕł░ńø«µĀć;µłæÕ╗║Ķ««µÉ£ń┤óµēƵ£ēÕÅ»ĶāĮńÜäĶĘ»ÕŠä’╝īńäČÕÉÄŌĆ£ÕÅæńö¤ŌĆØķĆÜĶ┐ćµØƵŁ╗Õ░ØĶ»ĢµŻĆµ¤źÕĘ▓ń╗ŵɣń┤óĶ┐ćńÜäõĮŹńĮ«ńÜäĶĘ»ÕŠäµØźµēŠÕł░µ£Ćńø┤µÄźńÜäĶĘ»ÕŠä’╝łµäÅÕæ│ńØĆÕģČõ╗¢ĶĘ»ÕŠäķ”¢ÕģłÕł░ĶŠŠķéŻķćī’╝īÕøĀµŁżµø┤ń¤Ł’╝ēŃĆé
- Õ»╗µēŠµ£Ćń¤ŁńÜäĶĘ»ÕŠä
- Aµś¤Õ«×µ¢Į’╝īµ▓Īµ£ēµēŠÕł░µ£Ćń¤ŁĶĘ»ÕŠäķŚ«ķóś
- õĖĆõĖ¬µśÄµś¤ń«Śµ│ĢŃĆéµēŠÕł░õĖƵØĪĶĘ»ÕŠäõĮåõĖŹµś»µ£Ćń¤ŁĶĘ»ÕŠä
- µ£Ćń¤ŁĶĘ»ÕŠäÕ«×µ¢ĮķŚ«ķóś
- µ▓Īµ£ēÕ»╗ĶĘ»ńÜäAµś¤Õ«×µ¢Į
- Aµś¤µ£Ćń¤ŁĶĘ»ÕŠäń«Śµ│Ģ
- Õ»╗µēŠµ£Ćń¤ŁĶĘ»ÕŠäõĮåµ£¬µŁŻńĪ«Ķ«Īń«ŚńÜ䵜¤Õ×ŗń«Śµ│Ģ
- ÕÅīÕÉæA *µ▓Īµ£ēµēŠÕł░µ£Ćń¤ŁĶĘ»ÕŠä
- A *’╝ła-star’╝ēÕÅæÕĖāµ£Ćń¤ŁĶĘ»ÕŠäńē╣Õ«Üńż║õŠŗ
- õĖƵś¤µ£Ćń¤ŁĶĘ»ÕŠäń«Śµ│ĢńÜäķŚ«ķóś
- µłæÕåÖõ║åĶ┐Öµ«Ąõ╗ŻńĀü’╝īõĮåµłæµŚĀµ│ĢńÉåĶ¦ŻµłæńÜäķöÖĶ»»
- µłæµŚĀµ│Ģõ╗ÄõĖĆõĖ¬õ╗ŻńĀüÕ«×õŠŗńÜäÕłŚĶĪ©õĖŁÕłĀķÖż None ÕĆ╝’╝īõĮåµłæÕÅ»õ╗źÕ£©ÕÅ”õĖĆõĖ¬Õ«×õŠŗõĖŁŃĆéõĖ║õ╗Ćõ╣łÕ«āķĆéńö©õ║ÄõĖĆõĖ¬ń╗åÕłåÕĖéÕ£║ĶĆīõĖŹķĆéńö©õ║ÄÕÅ”õĖĆõĖ¬ń╗åÕłåÕĖéÕ£║’╝¤
- µś»ÕÉ”µ£ēÕÅ»ĶāĮõĮ┐ loadstring õĖŹÕÅ»ĶāĮńŁēõ║ĵēōÕŹ░’╝¤ÕŹóķś┐
- javaõĖŁńÜärandom.expovariate()
- Appscript ķĆÜĶ┐ćõ╝ÜĶ««Õ£© Google µŚźÕÄåõĖŁÕÅæķĆüńöĄÕŁÉķé«õ╗ČÕÆīÕłøÕ╗║µ┤╗ÕŖ©
- õĖ║õ╗Ćõ╣łµłæńÜä Onclick ń«ŁÕż┤ÕŖ¤ĶāĮÕ£© React õĖŁõĖŹĶĄĘõĮ£ńö©’╝¤
- Õ£©µŁżõ╗ŻńĀüõĖŁµś»ÕÉ”µ£ēõĮ┐ńö©ŌĆ£thisŌĆØńÜäµø┐õ╗Żµ¢╣µ│Ģ’╝¤
- Õ£© SQL Server ÕÆī PostgreSQL õĖŖµ¤źĶ»ó’╝īµłæÕ”éõĮĢõ╗Äń¼¼õĖĆõĖ¬ĶĪ©ĶÄĘÕŠŚń¼¼õ║īõĖ¬ĶĪ©ńÜäÕÅ»Ķ¦åÕī¢
- µ»ÅÕŹāõĖ¬µĢ░ÕŁŚÕŠŚÕł░
- µø┤µ¢░õ║åÕ¤ÄÕĖéĶŠ╣ńĢī KML µ¢ćõ╗ČńÜäµØźµ║É’╝¤