Question

我正在寻找一种方法来使用Oracle数据库进行BITOR（）并且遇到了一个建议，只需使用BITAND（）代替BITOR（a，b）替换为+ b - BITAND（a，b）

我手工测试了几次并验证它似乎适用于我能想到的所有二进制数字，但我无法想出为什么这是正确的快速数学证明。
有人可以启发我吗？

Answer 1

A＆amp; B是在A和B中都打开的位组.A - （A＆amp; B）为您留下所有那些仅在A中打开的位。将B添加到该位，并获得所有打开的位在A中或在B中的那些。

简单地添加A和B将不起作用，因为携带两个都有1位。通过首先去除A和B共同的位，我们知道（A-（A＆amp; B））将没有与B共同的位，因此将它们加在一起可以保证不产生进位。

Answer 2

想象一下，您有两个二进制数：a和b。并且假设这些数字在同一时间内从不具有1，即如果a在某个位中具有1，则b在相应位中始终具有0。而在其他方向，如果b在某个位中有1，那么a在该位中始终为0。例如

a = 00100011
b = 11000100

这是满足上述条件的a和b的示例。在这种情况下，很容易看出a | b与a + b完全相同。

a | b = 11100111
a + b = 11100111

现在让我们取两个违反我们条件的数字，即两个数字在某个公共位中至少有一个

a = 00100111
b = 11000100

在这种情况下a | b与a + b相同吗？否

a | b = 11100111
a + b = 11101011

为什么他们不一样？它们是不同的，因为当我们+两个数字中都有1的位时，我们产生所谓的进位：结果位为0，并且1被传送到左边的下一位：1 + 1 = 10。操作|没有进位，因此1 | 1仅为1。

这意味着a | b和a + b之间的差异发生在且仅当数字在公共位中至少有一个1时。当我们将两个数字与1个公共位相加时，这些公共位会被“加”两次并产生一个进位，这会破坏a | b和a + b之间的相似性。

现在看看a & b。 a & b计算什么？ a & b生成的数字在a和b都有1的所有位中都为1.在我们的最新示例中

a =     00100111
b =     11000100
a & b = 00000100

如上所述，这些正是使a + b与a | b不同的位。 a & b中的1表示将发生进位的所有位置。

现在，当我们执行a - (a & b)时，我们有效地删除（减去）来自a的所有“违规”位并且只有这些位

a - (a & b) = 00100011

数字a - (a & b)和b没有共同的1位，这意味着如果我们添加a - (a & b)和b，我们就不会遇到进位，并且，如果你想一想，我们应该得到与我们刚刚a | b

一样的结果

a - (a & b) + b = 11100111

Answer 3

A＆amp; B = C，其中在C中设置的任何位是A和B中设置的位 A-C = D或B-C = E将这些公共位设置为0.没有携带效应，因为1-1 = 0。
D + B或E + A类似于A + B，只是因为我们先前减去了A和B，因为已经清除了D或E中所有常用的位，所以没有进位。

最终结果是A-A＆amp; B + B或B-A＆amp; B + A等同于A | B.

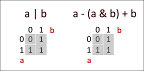
这是一个真值表，如果它仍然令人困惑：

 A | B | OR   A | B | &    A | B | -    A | B | + 
---+---+---- ---+---+---  ---+---+---  ---+---+---
 0 | 0 | 0    0 | 0 | 0    0 | 0 | 0    0 | 0 | 0  
 0 | 1 | 1    0 | 1 | 0    0 | 1 | 0-1  0 | 1 | 1
 1 | 0 | 1    1 | 0 | 0    1 | 0 | 1    1 | 0 | 1  
 1 | 1 | 1    1 | 1 | 1    1 | 1 | 0    1 | 1 | 1+1

注意+和 - 操作中的进位行，我们避免那些，因为A-（A＆amp; B）设置的情况都是A中的位，B中的A是1到0，然后从B中添加它们也带来其他情况是A或B中都有1，但两者都没有0，所以OR真值表和A-（A＆amp; B）+ B真值表是相同的。

另一种观察它的方法是看到A + B几乎像A | B，除了底行的进位。 A＆amp; B隔离了我们的底行，A-A和B将那些孤立的行隔离在+表中的两行，而（A-A＆amp; B）+ B等同于A | B.

虽然你可以将它转交给A + B-（A＆amp; B），但我担心可能出现溢出，但这似乎是不合理的：

#include <stdio.h>
int main(){ unsigned int a=0xC0000000, b=0xA0000000;
printf("%x %x %x %x\n",a,   b,       a|b,       a&b);
printf("%x %x %x %x\n",a+b, a-(a&b), a-(a&b)+b, a+b-(a&b)); }

c0000000 a0000000 e0000000 80000000
60000000 40000000 e0000000 e0000000

编辑：所以我在得到答案之前写了这个，然后我的家庭连接有两个小时的停机时间，我终于设法发布了它，之后才注意到它已经适当回答了两次。就个人而言，我更喜欢引用一个真值表来计算按位运算，所以我会留下它以防它帮助某人。

为什么（a | b）相当于 - （a＆amp; b）+ b？

4 个答案: