在C＃中将π计算为“无限”二进制精度

Question

到目前为止，看起来Fabrice Bellard的基础2方程式是可行的方式

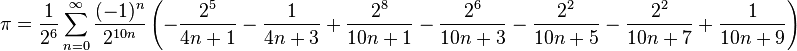
具有讽刺意味的是，这需要一个BigReal类型;我们有.Net这个吗？ .Net 4.0有BigInteger。

任何人都有Haskell版本吗？

Answer 1

因为你要求一个Haskell版本，here is a paper由Jerzy Karczmarczuk，称为“世界上最不可靠的技术来计算π”：

  

本文是一个非典型的练习   懒惰的功能编码，写作   有趣和指导。它可以阅读   并被任何人理解   理解编程语言   哈斯克尔。我们将展示如何实现   Bailey-Borwein-Ploue公式为π   以递归，渐进的方式   产生数字3,1,4,1，   5,9。 。直到记忆   疲惫。这不是一种方法   如果有人需要很多，请继续   数字！我们的编码策略是   不正常和危险，它   可证明是崩溃了。它基于   算术领域的算术   无限的数字序列   代表适当的分数扩大   在整数基数。我们展示如何   操纵：添加，乘以   整数等来自的序列   无限制地离开了，   这显然不能奏效   案件由于含糊不清。一些   深刻的哲学后果是   在结论中讨论过。

它并没有以高效或非常实用的方式真正解决问题，但是很有趣并且展示了懒惰无限精度算法的一些问题。

然后还有this paper by Jeremy Gibbons。

Answer 2

到目前为止，我最喜欢的Haskell pi用于来自Jeremy Gibbons：

pi = g(1,0,1,1,3,3) where
    g(q,r,t,k,n,l) = 
        if 4*q+r-t<n*t
        then n : g(10*q,10*(r-n*t),t,k,div(10*(3*q+r))t-10*n,l)
        else g(q*k,(2*q+r)*l,t*l,k+1,div(q*(7*k+2)+r*l)(t*l),l+2)

可以在以下网址找到证明该实施的数学背景：

A Spigot Algorithm for the Digits of Pi

Answer 3

维基百科详细介绍了获取pi here的数值近似的许多方法。他们还提供了一些示例伪代码

编辑：如果你对这种数学问题感兴趣而没有任何相关的现实世界问题需要解决（这绝对是一个很好的态度，恕我直言），你可以访问Euler Project page

Answer 4

存在基于DLR的动态语言处理大有理数的可能性（例如IronPython）。或者，您可以通过P/Invoke使用任何大型实数的可移植C / C ++实现。