我可以依赖PHP php.ini精确解决方案来解决浮点问题

时间：2013-01-29 16:17:21

标签： php floating-point

我在PHP中找到了floating point problem的一些解决方法：

php.ini设置precision = 14 

342349.23 - 341765.07 = 584.15999999992 // floating point problem

php.ini设置，让我们说precision = 8 

342349.23 - 341765.07 = 584.16 // voila!

演示：http://codepad.org/r7o086sS

那有多糟糕？

1。如果我只需要精确的2位数计算（金钱），我可以依赖这个解决方案吗？

2。如果没有，你可以在这个解决方案失败时为我提供一个明确的例子吗？

编辑：3。哪个php.ini.precision值最适合两位数，钱计算

  • 请注意我不能使用整数计算（浮点数* 100 =美分），这太迟了。
  • 我不打算处理高于10 ^ 6的数字
  • 我不需要比较数字

更新

@Baba答案很好，但他在测试中使用了precision=20，precision=6 ......所以我仍然不确定它是否会起作用。

请考虑以下事项：

我们说precision = 8，我唯一要做的就是添加+和减法-

A + B = C

A - B = C

问题1：对于0..999999.99之间的数字，精确解决方法是否会失败，其中A和B是带小数位的数字？如果是这样，请给我一个例子。

简单的测试可以完成这项工作：

// if it fails what if I use 9,10,11 ???
// **how to find when it fails??? **
ini_set('precision', 8); 
for($a=0;$a<999999.99;$a+=0.01) {
  for($b=0;$b<999999.99;$b+=0.01) {
     // mind I don't need to test comparision (round($a-$b,2) == ($a-$b))
     echo ($a + $b).','.($a - $b)." vs ";
     echo round($a + $b, 2).','.round($a - $b, 2)."\n";
  }
}

but obviously 99999999 * 2 is too big job so I can't run this test

问题2：如何估算/计算精确解决方法何时失败？没有这样疯狂的测试？ 是否有任何数学*，直接的答案？如何计算是否会失败？

*我不需要知道浮点计算的工作原理，但是当你知道精确度和A和B的范围时，解决方法失败

请注意我真的知道美分和bcmath是最佳解决方案。但我仍然不确定是否会因为减法和添加而失败或无法解决

5 个答案:

答案 0 :(得分：42)

简介

浮点运算被很多人认为是一个深奥的主题。这是相当令人惊讶的，因为浮点在计算机系统中无处不在。大多数小数都没有精确表示为二进制小数，因此有一些舍入。一个好的开始是What Every Computer Scientist Should Know About Floating-Point Arithmetic

问题

问题1

  

如果我只需精确的2位数计算（钱），我可以依赖此解决方案吗？

答案1

如果您需要精确2位，则答案为否您无法使用php精度设置来确定 2位小数即使你是not going to work on numbers higher than 10^6，所有的时间。

在计算过程中，如果长度小于8，则可能会增加精度长度

问题2

  

如果没有，你可以在这个解决方案失败时为我提供一个明确的例子吗？

答案2 

ini_set('precision', 8); // your precision
$a =  5.88 ; // cost of 1kg
$q = 2.49 ;// User buys 2.49 kg
$b = $a * 0.01 ; // 10% Discount only on first kg ;
echo ($a * $q) - $b;

输出

14.5824 <---- not precise 2 digits calculations even if precision is 8

问题3

  

哪个php.ini.precision值最适合两位数，钱计算？

回答3

精确度和资金计算是两个不同的事情......使用PHP精度作为财务计算或浮点长度的基础不是一个好主意

简单测试

请使用bcmath，number_format和简单minus

一起运行一些示例

Base 

$a = 342349.23;
$b = 341765.07;

<强> Example A 

ini_set('precision', 20); // set to 20 
echo $a - $b, PHP_EOL;
echo floatval(round($a - $b, 2)), PHP_EOL;
echo number_format($a - $b, 2), PHP_EOL;
echo bcsub($a, $b, 2), PHP_EOL;

输出

584.15999999997438863
584.15999999999996817    <----- Round having a party 
584.16
584.15  <-------- here is 15 because precision value is 20

<强> Example B 

ini_set('precision', 14); // change to  14 
echo $a - $b, PHP_EOL;
echo floatval(round($a - $b, 2)), PHP_EOL;
echo number_format($a - $b, 2), PHP_EOL;
echo bcsub($a, $b, 2), PHP_EOL;

输出

584.15999999997
584.16
584.16
584.16  <-------- at 14 it changed to 16

<强> Example C 

ini_set('precision', 6); // change to  6 
echo $a - $b, PHP_EOL;
echo floatval(round($a - $b, 2)), PHP_EOL;
echo number_format($a - $b, 2), PHP_EOL;
echo bcsub($a, $b, 2), PHP_EOL;

输出

584.16
584.16
584.16
584.00  <--- at 6 it changed to 00

<强> Example D 

ini_set('precision', 3); // change to 3
echo $a - $b, PHP_EOL;
echo floatval(round($a - $b, 2)), PHP_EOL;
echo number_format($a - $b, 2), PHP_EOL;
echo bcsub($a, $b, 2), PHP_EOL;

输出

584
584
584.16   <-------------------------------- They only consistent value 
0.00  <--- at 3 .. everything is gone

结论

忘记浮点数，然后只计算cents，然后再计算100，如果为时已晚，只需使用number_format，它看起来与我一致。

更新

  

问题1：对于0到999999.99之间的数字，精确解决方法是否会失败，其中A和B是带小数位的数字？如果是这样，请给我一个例子

表格0到999999.99，0.01的增量约为99,999,999，你的循环的组合可能性为9,999,999,800,000,000我真的不认为任何人我想为你做这样的测试。

由于浮点数是有限精度的二进制数，试图设置precision对确保准确性的影响有限这是一个简单的测试：

ini_set('precision', 8);

$a = 0.19;
$b = 0.16;
$c = 0.01;
$d = 0.01;
$e = 0.01;
$f = 0.01;
$g = 0.01;

$h = $a + $b + $c + $d + $e + $f + $g;

echo "Total: " , $h , PHP_EOL;


$i = $h-$a;
$i = $i-$b;
$i = $i-$c;
$i = $i-$d;
$i = $i-$e;
$i = $i-$f;
$i = $i-$g;

echo $i , PHP_EOL;

输出

Total: 0.4
1.0408341E-17     <--- am sure you would expect 0.00 here ;

尝试

echo round($i,2) , PHP_EOL;
echo number_format($i,2) , PHP_EOL;

输出

0
0.00    <------ still confirms number_format is most accurate to maintain 2 digit
  

问题2：如何估算/计算精确解决方法何时失败？没有这样疯狂的测试？有没有数学*，直接的答案呢？如何计算是否会失败？

事实上，Floating Point Accuracy Problems仍有Machine precision and backward error analysis，但对于数学解决方案，您可以查看

  

我不需要知道浮点计算的工作原理，但是当你知道精确度和A和B的范围时，解决方法失败

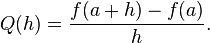
enter image description here

不确定该陈述的含义：）

答案 1 :(得分：4)

我只是引用this有趣的网站来解决这个问题。 （没有预期的声誉:)但应该提到：

  

我该怎么做才能避免这个（浮点）问题？

     

这取决于你正在做什么样的计算。

     
      

  • 如果您确实需要将结果准确添加，尤其是在您使用时   money：使用特殊的十进制数据类型。

    •   

  • 如果您只是不想看到所有这些额外的小数位：只需在结果显示时将结果四舍五入到固定的小数位数。

    •   

  • 如果没有可用的十进制数据类型，另一种方法是使用整数，例如：完全以美分进行货币计算。但这是更多的工作，并有一些缺点。

    •   

该网站还包含PHP

的一些基本提示

我会使用整数或为它创建一个特殊的Decimal类型。

如果您决定使用 bcmath ：如果将该值传递给SQL查询或其他外部程序，请小心。如果他们不了解精确度，可能会导致不必要的副作用。 （很可能）

答案 2 :(得分：3)

根据文档，precision directive只会更改将数字转换为字符串时显示的数字：

  

精确度 integer
      浮点数中显示的有效位数。

所以它基本上是number_format()或money_format()的一个非常复杂的替代品，除了它有更少的格式化选项，它可能会受到一些您可能不知道的其他副作用：

<?php

$_POST['amount'] = '1234567.89';

$amount = floatval($_POST['amount']);
var_dump($amount);

ini_set('precision', 5);
$amount = floatval($_POST['amount']);
var_dump($amount);

... 

float(1234567.89)
float(1.2346E+6)

修改

我坚持认为：此设置不会改变PHP使用数字进行数学计算的方式。当将从浮点数（甚至不是整数！）转换为字符串时，这只是一种神奇的方式来更改格式选项。例如：

<?php

ini_set('precision', 2);

$amount = 1000;
$price = 98.76;
$total = $amount*$price;

var_dump($amount, $total);

ini_set('precision', 15);
var_dump($amount, $total);

...打印：

int(1000)
float(9.9E+4)
int(1000)
float(98760)

其中说明了：

  1. 浮点计算不受影响，只有显示更改
  2. 整数在所有情况下都不受影响

答案 3 :(得分：1)

我相信如果您只想简化您的结果，那么无需在服务器范围内对您的配置进行更改即可解决您的浮点问题。

round(342349.23 - 341765.07, 2) = 584.16

答案 4 :(得分：0)

如果使用precision = 8，如果使用8位数字，则无法确定第8位数字。将第9位数字舍入为1可以取消。

例如

12345678.1 -> 12345678
12345678.9 -> 12345679

这可能看起来不那么糟糕，但请考虑

   (11111111.2 + 11111111.2) + 11111111.4
-> (11111111)                + 11111111.4
-> 22222222.4
-> 22222222

然而，如果你使用的是precision = 9，那么这将是22222222.8，它会转到22222223。

如果你只是做加法和减法，你应该使用至少2个左右的精度数字，以避免在这些类型的计算中舍入。如果你正在进行乘法或除法，你可能需要更多。使用必要的最低限度可能会导致数字丢失。

所以，为了回答你的问题，如果你很幸运，你可能会侥幸逃脱，并且php在计算中使用高精度，然后只以较低的精度存储结果（然后你不用那个数字去并且进行其他计算），但总的来说，这是一个非常糟糕的主意，因为（至少）计算中的最后一位数字是完全不可靠的。

相关问题
最新问题