在Fibonacci序列中,是fib(0)0还是1?
我正在做一个主题的任务是fib(0)被定义为= 1.但那不可能是对的? fib(0)是0?
Program with fib(0) = 1; spits out fib(4) = 5
Program with fib(0) = 0; spits out fib(3) = 3
正确的定义是什么?
10 个答案:
答案 0 :(得分:25)
Fib(0)= 1的定义称为组合定义,Fib(0)= 0是经典定义。两者都在Fibonacci Quarterly中使用,尽管使用组合定义的作者需要添加一个解释句子。真实计数中的Benjamin和Quinn使用f_n表示第n个组合Fibonacci数,使用F_n表示第n个经典Fibonacci数。组合定义很好,对于计算诸如“有多少种方式可以走n步,一次采取一个或两个步骤?”这样的问题并不奇怪。当n为0时,有一种方法可以做到,而不是零方式。
答案 1 :(得分:20)
你是对的。使用种子值fib(0) = 0和fib(1) = 1定义Fibonacci sequence。这是要求其余序列正确的。
fib(0) = 1可以使用的唯一条件是,如果您定义了“基于-1的计数系统”(与通常的基于0和基于1的约定相反)。这很古怪,但我相信你同意。
答案 2 :(得分:10)
来自维基百科上的Fibonacci number条目:
在数学中,斐波纳契数 是以下数字序列:

根据定义,前两个斐波那契 数字是0和1,每个 剩余数量是总和 前两个。 有些消息来源省略了 初始0,而不是开始 两个1s的序列。
在数学术语中,序列Fn 斐波纳契数的定义由 复发关系
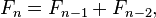
有种子值
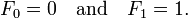
答案 3 :(得分:6)
根据Fibonacci序列的定义,您可以生成用于定义第n个元素的封闭形式:
F(n) = ( f^n - (1-f)^n ) / sqrt(5),
where f = (1 + sqrt(5)) / 2 [the golden ratio]
对于n = 0,显然是0:
F(0) = (1 - 1) / sqrt(5) = 0.
答案 4 :(得分:4)
http://en.wikipedia.org/wiki/Fibonacci_number
Fibonacci自己开始了1而不是0的序列。重要的是要认识到一个人的意见不是不可改变的事实,并且可能值得考虑你不一定知道比创建序列的人更好。我觉得用0开始序列是没关系的,只要你不这样做是唯一绝对正确的做事方式,就像#"索引0&#的数字一样34;从根本上来说是模棱两可的,应该明确地进行沟通。
" index"的问题仅适用于我们而非斐波那契。因此,如果我们想要使用他的起始编号并且我们使用基于0的索引,我们将他的起始编号放在索引0处,或者如果我们使用基于1的索引,我们将使用基于1的索引。 d将他的起始编号放在索引1处。
并且由于确实可以将序列继续向左,这也使得从0完全任意开始。为什么不从-1开始并转-1,1,0,1,1,2 ......?
答案 5 :(得分:3)
他们都是正确的。如果您指定序列G {n} 递归G {1} = 3,G {2} = 5,G {n} = G {n - 1} + G {n - 2} 然后大多数人会同意这是“斐波那契序列”。 唯一的区别是前面几个术语,但是 领先的术语大多与任何有趣的无关 关于序列的问题。斐波那契的核心 sequence是添加规则,以及使用的任何序列 该规则是斐波纳契数列。这是必要的 如果你指定0是否在序列中 想询问有关特定指数的具体问题...... 其他每件事都只是对索引的翻译 几乎无关紧要。也就是说,如果问题是 '找到一个封闭的形式解决方案的第N个值 序列',然后解决它将解决问题 对于F而言,只需简单地移动解决方案。该 这两个序列的问题很难解决。
答案 6 :(得分:3)
你不能拥有零兔,从而产生一对,并且“从一对开始每年生产多少对兔子,从第二个月开始每月繁殖”是斐波那契的原始问题。
答案 7 :(得分:0)
fib 0 = 0
fib 1 = 1
这是种子价值定义。
答案 8 :(得分:0)
我的解释是针对那些希望对该系列和零期限有简单理解的程序员的。
从
开始first term as f(1) = 1
second term as f(2) = f(1)+nothing Available = f(1)+0 = 1+0 =1
third term as f(3) = f(2)+f(1) = 1+1 = 2
可以相信,负数和零项是使用黄金比率的斐波那契公式的结果
黄金比率(GR)值为1.618034,公式为f(n) = (GR^n - (1-GR)^n))/sqrt(5)
答案 9 :(得分:0)
斐波那契数列不是以0开头,而是以1开头。
试图将数学概念表示为计算机程序,我们感到困惑。术语“ Fib(0)”是包含始终为1的第一个斐波那契数的数组索引。
我们之所以问这个问题,是因为当有人输入0作为输入时,我们必须从程序中返回一些内容。该输入实质上意味着生成0斐波那契数。因此,您返回一条消息,提示“未生成斐波那契数字”
- 我写了这段代码,但我无法理解我的错误
- 我无法从一个代码实例的列表中删除 None 值,但我可以在另一个实例中。为什么它适用于一个细分市场而不适用于另一个细分市场?
- 是否有可能使 loadstring 不可能等于打印?卢阿
- java中的random.expovariate()
- Appscript 通过会议在 Google 日历中发送电子邮件和创建活动
- 为什么我的 Onclick 箭头功能在 React 中不起作用?
- 在此代码中是否有使用“this”的替代方法?
- 在 SQL Server 和 PostgreSQL 上查询,我如何从第一个表获得第二个表的可视化
- 每千个数字得到
- 更新了城市边界 KML 文件的来源?