计算ctr时如何避免印象偏差？

Question

当我们训练ctr（点击率）模型时，有时我们需要从历史数据中计算出真实的ctr，就像这样

                 #(click)
    ctr   =  ----------------
              #(impressions)

我们知道，如果展示次数太少，则计算的ctr不是真实的。因此，我们始终设置一个阈值来过滤掉足够大的展示次数。

但我们知道印象越高，对ctr的信心越高。然后我的问题是：是否有一个印象规范化的统计方法来计算ctr？

谢谢！

Answer 1

您可能需要为估计的ctr表示置信区间。 Wilson score interval是一个很好的尝试。

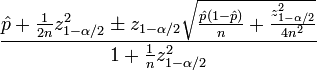
您需要低于统计数据来计算置信度分数：

• \hat p是观察到的ctr（#clicked vs #impressions的分数）
• n是总展示次数
• z _{α/ 2} 是标准正态分布的(1-α/2)分位数

下面显示了python中的一个简单实现，我使用z _{（1-α/ 2）} = 1.96，它对应于95％的置信区间。我在代码的末尾添加了3个测试结果。

# clicks      # impressions       # conf interval
2             10                  (0.07, 0.45)
20            100                 (0.14, 0.27)
200           1000                (0.18, 0.22)

现在您可以设置一些阈值以使用计算的置信区间。

from math import sqrt

def confidence(clicks, impressions):
    n = impressions
    if n == 0: return 0
    z = 1.96 #1.96 -> 95% confidence
    phat = float(clicks) / n
    denorm = 1. + (z*z/n)
    enum1 = phat + z*z/(2*n)
    enum2 = z * sqrt(phat*(1-phat)/n + z*z/(4*n*n))
    return (enum1-enum2)/denorm, (enum1+enum2)/denorm

def wilson(clicks, impressions):
    if impressions == 0:
        return 0
    else:
        return confidence(clicks, impressions)

if __name__ == '__main__':
    print wilson(2,10)
    print wilson(20,100)
    print wilson(200,1000)

"""    
--------------------
results:
(0.07048879557839793, 0.4518041980521754)
(0.14384999046998084, 0.27112660859398174)
(0.1805388068716823, 0.22099327100894336)
"""

Answer 2

如果将此视为二项式参数，则可以进行贝叶斯估计。如果您之前的ctr是统一的（带有参数（1,1）的Beta分布）那么您的后验是Beta（1 +＃click，1 + #impressions- #Click）。你的后验意思是＃click + 1 / #impression + 2，如果你想要一个这个后验的统计数据统计，但你可能没有，这就是原因：

我不知道你用什么方法来确定ctr是否足够高，但是让我们说你对ctr＆gt;的一切感兴趣。 0.9。然后，您可以使用β分布的累积密度函数来查看概率质量超过0.9阈值的比例（这将是1 - cdf为0.9）。通过这种方式，由于样本量有限，您的阈值自然会包含估算的不确定性。

Answer 3

计算此置信区间的方法有很多种。 Wilson分数的另一种选择是Clopper-Perrson区间，我发现它在电子表格中很有用。

Upper Bound Equation

Lower Bound Equation

其中

• B()是Inverse Beta Distribution
• alpha是置信度错误（例如95％置信度，alpha为5％）
• n是样本数量（例如展示次数）
• x是成功次数（例如点击次数）

在Excel中，B()公式提供BETA.INV的实施。

Google表格中没有B（）的等效公式，但可以从JavaScript统计库中修改Google Apps脚本自定义函数（例如，为jstat搜索github）