对Newton Raphson的初步猜测

Question

如何根据A，B和C确定等式Ax+Bsin(x)=C的初始猜测？ 我试图用Newton Raphson来解决它。 A，B和C将在运行时给出。

为此目的，还有其他方法比Newton Raphson更有效吗？

Answer 1

最佳初始猜测是根本身，因此找到“最佳”猜测并不是真正有效。

任何猜测都会为您提供有效的解决方案，只要f'(x0) != 0为任何步骤，只发生在cos(x)的零，k*pi + pi/2为任何整数k }}

我会尝试x0 = C * pi，看看它是否有效。

然而，你最大的问题是你的功能的周期性。对于你的函数，牛顿的方法会很慢（如果它甚至有用），因为sin(x)会一遍又一遍地来回移动x0。

---

<强>注意事项：

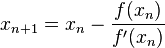
在Newton的方法中，您是否注意到f'(xn)在分母中是怎样的？ f'(x)无限次地接近0次。如果您的f'(x) = 0.0001（或任何接近零的地方，有可能发生），您xn+1的距离会远离xn。

更糟糕的是，由于f'(x)是一个周期函数，这可能会反复发生，这意味着牛顿的方法可能永远不会收敛于任意x0。

Answer 2

最简单的“好”近似是假设sin（x）近似为零，因此设置：

x0 = C/A

Answer 3

好吧，如果A，B和C是真实的并且与0不同，那么(B+C)/A是最高根的上引号，(C-B)/A是最低根的下引号，{{{ 1}}。你可以从那些开始。

Answer 4

牛顿法可以用于任何猜测。问题很简单， 如果有一个等式，我猜测x0 = 100 最好的解决方案是x0 = 2 我知道答案是2.34 * 通过使用世界上的任何猜测，你最终将达到2.34 * 该方法说要选择一个猜测因为没有有效的猜测它会采取许多不舒服的解决方案没有人想重复该方法20次  并且猜测解决方案并不难 你只是找到一个关键点 - 例如，3太大而2太小 所以答案在2到3之间 但如果反而猜测2你猜50 你仍然可以找到正确的解决方案。 就像我说它会花费你更长的时间 我自己测试了这个方法 我猜测1000随机方程 我知道最好的猜测是4 答案是在4到5之间 我选择1000我花了很多时间 但几个小时后，我从1000下降到了4.something 如果你以某种方式找不到关键点，你实际上可以将一个随机数等于x0然后最终你会得到正确的解决方案 无论你猜到了什么数字。