Question

我有一个等式g = @(x)(5-((5/2)*exp(x/2))-((7/2).x^2)-3*x).^1/3，并且根据规格，该等式有3个根。但我的输出在x和g（x）之间没有任何匹配，以获得固定点。输出：

>> fpi1(g, 0.5, 20)
   x0                                           g(x0)
  0.500000000000000                       0.670818823114861 - 1.161892284308499i
  0.670818823114861 - 1.161892284308499i  1.281297751181495 - 1.559064591427071i
  1.281297751181495 - 1.559064591427071i  1.864118571141893 - 1.621766955715062i
  1.864118571141893 - 1.621766955715062i  2.320549078066838 - 1.504496934526923i
  2.320549078066838 - 1.504496934526923i  2.646646533032701 - 1.316018792060223i
  2.646646533032701 - 1.316018792060223i  2.870437643388612 - 1.115036747500670i
  2.870437643388612 - 1.115036747500670i  3.021682102842603 - 0.927806240969038i
  3.021682102842603 - 0.927806240969038i  3.123528510261589 - 0.763760920462736i
  3.123528510261589 - 0.763760920462736i  3.192243659445853 - 0.624547007383635i
  3.192243659445853 - 0.624547007383635i  3.238827490411373 - 0.508525243060542i
  3.238827490411373 - 0.508525243060542i  3.270613725640807 - 0.412880979787002i
  3.270613725640807 - 0.412880979787002i  3.292471687008435 - 0.334576282706924i
  3.292471687008435 - 0.334576282706924i  3.307635263738642 - 0.270756021961336i
  3.307635263738642 - 0.270756021961336i  3.318257296190301 - 0.218898831715851i
  3.318257296190301 - 0.218898831715851i  3.325776161489184 - 0.176850650328430i
  3.325776161489184 - 0.176850650328430i  3.331157314339334 - 0.142806525903066i
  3.331157314339334 - 0.142806525903066i  3.335052371178708 - 0.115272146831085i
  3.335052371178708 - 0.115272146831085i  3.337903988543196 - 0.093020017690524i
  3.337903988543196 - 0.093020017690524i  3.340015124633794 - 0.075047094363536i
  3.340015124633794 - 0.075047094363536i  3.341594884710001 - 0.060536697645525i
  3.341594884710001 - 0.060536697645525i  3.342788954448884 - 0.048825574318716i

我做错了什么？怎么可能修好？

%Program 1.2 Fixed-Point Iteration
%Computes approximate solution of g(x)=x
%Input: inline function g, starting guess x0, 
%       number of steps k
%Output: Approximate solution xc
function xc=fpi1(g,x0,k)
x(1)=x0;
for i=1:k
  x(i+1)=g(x(i));
end
xc=x(k+1);
disp('   x0                                           g(x0)');
disp([x', g(x)']);

Answer 1

在我开始之前只是一个小小的注释。您的g函数中存在拼写错误。我假设您的意思是(7/2)*而不是(7/2).。我还必须编辑你的代码以允许电源操作按元件工作：

g = @(x)(5-((5/2).*exp(x/2))-((7/2)*x.^2)-3*x).^1/3;

使用此更正功能进行一些初步测试可与您获得的功能相匹配。

在任何情况下，使用定点迭代来查找等式的根是不正确的。在我进入你需要做的修复之前，我想介绍定点迭代的工作方式，以便你（以及阅读这篇文章的其他人）了解我来自哪里

定点迭代基于初始输入值x0。然后，在将此值提交到函数中后，重复计算此值的输出，然后在下一次迭代中重复输出作为输入。具体而言，定点迭代方案执行此操作：

^{来源：Wikipedia}

理想情况下，经过一些迭代后，我们希望迭代收敛到某个值x，这样：

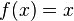
^{来源：Wikipedia}

以上是定点的定义。要做到这一点以找到根不是（原生）支持的，因为找到一个等式的根与固定点应该是什么相矛盾。根目录的定义是f(x) = 0，而不是定点，除非x=0 。如果要使用定点迭代来查找根，则必须更改函数f的结构方式。这导致我们使用称为Newton's Method的经典迭代根发现技术，该技术也使用定点迭代来查找函数的根，但函数f(x)是不同的。

我不会进入牛顿方法的推导，但这是你在每次迭代时所做的事情：

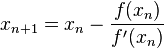
^{来源：Wikipedia}

f(x)是函数，f'(x)是f(x)的衍生物。如果我们用新函数g(x)替换右侧，那么您将对函数g(x)执行定点迭代，并且收敛后的结果是您正在寻找的根。具体而言，如果：

^{来源：Wikipedia}

然后：

^{来源：Wikipedia}

因此：

^{来源：Wikipedia}

... x是函数f(x)的根，如果：

^{来源：Wikipedia}

因此，您需要修改代码，以便它不再使用函数句柄。它必须采用符号版本，因为您需要使用函数的派生。

请注意，这是您需要对代码进行修改才能使其正常工作：

%//Program 1.2 Fixed-Point Iteration via Newton's Method
%//Computes approximate root of g(x)=0
%//Input: symbolic function g, starting guess x0, 
%//       number of steps k
%//Output: Approximate solution xc

format long g; %// For precision
x(1)=x0;
gp = diff(g); %// Change
for i=1:k
    gval = double(subs(g, 'x', x(i))); %// Change
    gpval = double(subs(gp, 'x', x(i))); %// Change
    x(i+1)= x(i) - (gval/gpval); %// Change
end
xc=x(k+1);
y = double(subs(g, 'x', x)); %// Change
disp('                        x0                      g(x0)');
disp([x' y'])

与函数内部不同的是，您可以使用diff符号找到派生词。此外，如果要将值替换为函数，则需要使用subs，然后将结果转换为double。我还假设你的函数是关于变量x的。

第三行代码会将您累积的所有x值转换为double数组以供显示。

要运行此代码，您可以：

syms x;
g = (5-((5/2)*exp(x/2))-((7/2)*x^2)-3*x)^1/3;
xc = fpi(g, 0.5, 20);

请注意，您不再需要元素操作符，因为我们正在处理符号方程式。

我们得到：

>> fpi(g, 0.5, 20)
                        x0                      g(x0)
                       0.5        -0.195021180573118
         0.427814775036064       -0.0067677938874851
          0.42512303212814     -9.38738903072792e-06
         0.425119288112029     -1.81600035806892e-11
         0.425119288104786     -5.28061163184459e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17

因此其中一个根等于0.425119288104786。右栏告诉您每次迭代时g(x)的值是什么，并且您可以看到它非常小...几乎为0.这就是根的定义更多或更少。

通过固定点迭代查找根时输出错误

1 个答案: