需要关于图解决问题的简单建议

Question

我的一位同事向我提出了一个来自在线法官网站的练习，该网站基本上解决了一个小城镇疏散计划的问题。

我不需要答案（也不需要它）我只需要一个建议，哪个是解决它的最佳方法，因为我对这类问题有点新意。

该问题包括城镇建筑物，如果发生核攻击，有工人和防尘罩。我必须建立一个算法，将每个建筑物的工人分配到一个或多个防辐射庇护所，但是某些庇护所不会变得过于拥挤，而其他庇护所几乎是空的（否则我只会让工人去最近的一个）

问题是：http://acm.timus.ru/problem.aspx?space=1&num=1237

如果它的离线版本是谷歌缓存版本：http://webcache.googleusercontent.com/search?q=cache:t2EPCzezs7AJ:acm.timus.ru/problem.aspx%3Fspace%3D1%26num%3D1237+vladimir+kotov+evacuation+problem&cd=1&hl=pt-PT&ct=clnk&gl=pt

到目前为止，我所做的是为每栋建筑物提供最近的避难所，并将该建筑物的工人数量等于避难所的容量。然后移动到下一个建筑物。但有时工人的数量大于避难所的容量，在这种情况下，我遍历每个建筑物，生病只是迭代然后再次使用相同的算法，直到每个建筑物都有0个工人，问题是这不是最好的方法解决它。

欢迎任何提示，请不要因为我要求答案，我只是想在正确的解决方向上提出建议。

提前感谢。

Answer 1

这看起来像<{3>} 完全，可以（显然）使用线性编程来解决。 （我说显然，因为这看起来是整数线性编程的一个实例）。

来自网站：

  

标准场景中的a   运输问题出现了   发送产品的单位   连接的高速公路网络   给定一组城市。每个城市都是   被视为“来源”，在   这些单位将从中运出   在那里，或作为“下沉”，在那些单位   在那里被要求。每个来源都有一个   给定供应，每个水槽都有一个给定的   需求，以及连接的每条高速公路   源 - 汇对具有给定的   每单位运输成本   装船。这可以在中看到   网络的形式，如图所示   图TP-1如下。

  

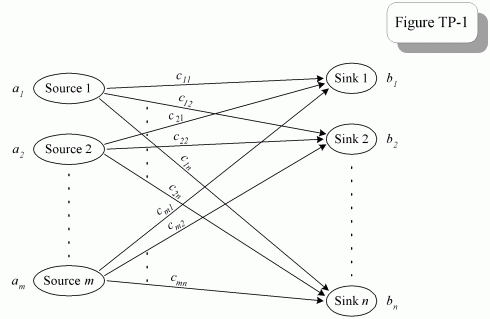
鉴于这样的网络，问题   兴趣是确定最佳   最小化的运输方案   主题为出货总成本   供应和需求限制。

希望有所帮助。

Answer 2

这看起来像是一个标准的Min-cost max flow问题。具有约200个顶点的二分图应该能够及时运行。

要创建顶点约束（每个节点只能处理k个人），您只需创建第二个图形G_1，在其中为每个v_i添加一个额外的顶点u_i - 并且将流量v_i设置为u_i，无论您的约束是什么，在这种情况下，k + 1，成本为0.所以基本上如果原始图G中存在边（a，b），那么在G_1中，每个都有一个边（u_a，v_b）边缘。实际上，您正在创建第二层顶点，将每个顶点的流限制为k。