如何在MATLAB中找到斜率（速率）？

Question

如何在MATLAB中找到斜率（速率）？

例如，假设我有散点图：

Year = [2001 2002 2003 2004 2005];
Distance = [1.5 1.8 1.9 2.2 2.5];
scatter(Year, Distance)
hold on
pf = polyfit(Year,Distance,1);
f = polyval(pf,Year);
plot(Year,f)

我可以通过以下方式找到R：

[r,p] = corrcoef(Year,Distance)

我想找到每年距离增加的速度，我认为这相当于斜率？

Answer 1

在这种情况下，您对斜率的解释是正确的。如果以这种方式使用polyfit，则会找到最适合该分布的回归线的斜率和截距。在这种情况下，斜率将是每年距离增加的速率。在不详细说明的情况下，polyfit将确定最佳拟合线，以最小化最佳拟合线与数据点之间的平方误差之和。因此，根据您的点数分布，此斜率将为您提供每年距离增加的最佳率。

你可以按照Chris A的方法，你可以找到逐点的相邻点并为每个点计算一个斜率，然后做一个平均值，但做polyfit会找到最小二乘回归并且在我看来，这是最佳选择。

您可以通过提取已经观察到的pf的第一个值来获得最小二乘法或最佳拟合斜率。第二个值将包含回归线的截距项。

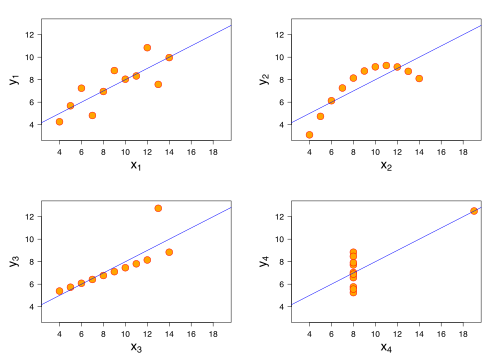
使用corrcoef确定合适程度的好选择。但是，要小心并将相关系数与一粒盐相结合。某些分布可能会报告良好的相关系数，但实际最佳拟合线看起来不会很好。一个典型的例子是Anscombe quartet。在这个例子中，所有分布报告的相关系数为0.816，但数据的可变性却完全不同。作为一种自我遏制手段，这就是数据的外观以及每组点的最佳拟合线。您可以看到回归线对于所有数据集实际上是相同的，但点分布完全不同：