在Matlab中查找具有噪声数据的近似局部最大值

Question

matlab FAQ描述了一种查找局部最大值的单行方法：

index = find( diff( sign( diff([0; x(:); 0]) ) ) < 0 );

但我相信这只有在数据或多或少光滑的情况下才有效。假设您有数据以小间隔上下跳跃但仍有一些近似的局部最大值。你会如何找到这些点？您可以将矢量划分为n个片段并找到不在每个片段边缘的最大值，但应该有更优雅和更快的解决方案。

单线解决方案也很棒。

编辑：我正在处理嘈杂的生物图像，我试图分成不同的部分。

Answer 1

我不确定您正在处理哪种类型的数据，但这是我用于处理语音数据的方法，可以帮助您找到局部最大值。它使用信号处理工具箱中的三个功能：HILBERT，BUTTER和FILTFILT。

data = (...the waveform of noisy data...);
Fs = (...the sampling rate of the data...);
[b,a] = butter(5,20/(Fs/2),'low');  % Create a low-pass butterworth filter;
                                    %   adjust the values as needed.
smoothData = filtfilt(b,a,abs(hilbert(data)));  % Apply a hilbert transform
                                                %   and filter the data.

然后，您将在 smoothData 上执行最大值查找。首先使用HILBERT在数据上创建一个正包络，然后FILTFILT使用BUTTER的滤波器系数对数据包络进行低通滤波。

有关此处理如何工作的示例，这里有一些图像显示了一段录制语音的结果。蓝线是原始语音信号，红线是信封（使用HILBERT获得），绿线是低通滤波结果。底部图是第一个的放大版本。

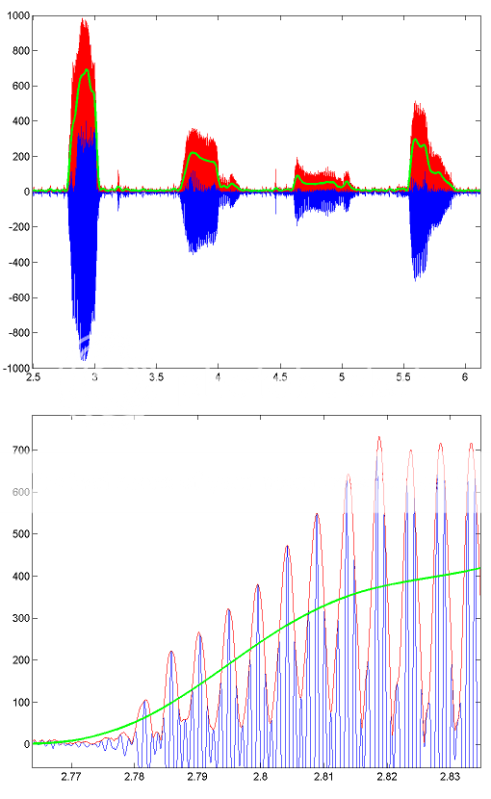
有些随意可以尝试：

这是我最初的一个随意的想法...你可以尝试通过找到最大值的最大值来重复这个过程：

index = find(diff(sign(diff([0; x(:); 0]))) < 0);
maxIndex = index(find(diff(sign(diff([0; x(index); 0]))) < 0));

然而，根据信噪比，我们不清楚需要多少次才能获得你感兴趣的局部最大值。这只是一个随机的非过滤选项。 =）

MAXIMA FINDING：

万一你好奇，我见过的另一个单行最大值搜索算法（除了你列出的那个）：

index = find((x > [x(1) x(1:(end-1))]) & (x >= [x(2:end) x(end)]));

Answer 2

根据您的需要，过滤噪声数据通常很有帮助。请查看MEDFILT1，或使用CONV以及FSPECIAL。在后一种方法中，您可能希望使用CONV的“相同”参数和FSPECIAL创建的“高斯”过滤器。

完成过滤后，通过最大值查找器输入。

编辑： 运行时复杂性

假设输入向量的长度为X，滤波器内核的长度为K.

中值过滤器可以通过执行运行插入排序来工作，因此它应该是O（X K + K log K）。我没有查看源代码，其他实现是可能的，但基本上它应该是O（X K）。

当K很小时，conv使用直接的O（X * K）算法。当X和K几乎相同时，使用快速傅立叶变换会更快。该实现是O（X log X + K log K）。 Matlab足够智能，可根据输入大小自动选择正确的算法。

Answer 3

如果您的数据大量跳跃，那么该函数将具有许多局部最大值。 所以我假设你不想找到所有的局部最大值。但是你对本地最大值的标准是什么？如果你有一个标准，那么可以为此设计一个方案或算法。

我现在猜测，您可能应首先对数据应用低通滤波器，然后找到局部最大值。虽然过滤后局部最大值的位置可能与之前的位置不完全对应。

Answer 4

有两种方法可以查看此类问题。人们可以将这看作主要是平滑问题，使用滤波工具来平滑数据，然后使用各种插值（可能是插值样条）进行插值。找到插值样条的局部最大值是一件容易的事情。 （请注意，这里通常应该使用真正的样条曲线，而不是pchip插值。在interp1中指定“立方”插值时使用的方法Pchip将无法准确定位位于两个数据点之间的局部最小值。）

这种问题的另一种方法是我倾向于选择的方法。这里使用最小二乘样条模型来平滑数据并产生近似而不是插值。这种最小二乘样条具有允许用户进行大量控制以将其对问题的了解引入模型的优点。例如，科学家或工程师通常具有关于所研究过程的信息，例如单调性。这可以构建到最小二乘样条模型中。另一个相关选项是使用平滑样条曲线。它们也可以通过内置的正则约束来构建。如果您有样条曲线工具箱，那么spap2将具有一些适用于样条曲线模型的实用程序。然后fnmin会找到一个最小化器。 （可以从最小化代码中轻松获得最大化。）

当数据点间隔相等时，采用滤波方法的平滑方案通常最简单。不等间距可能会推动最小二乘样条模型。另一方面，结点放置可能是最小二乘样条的问题。我在所有这一点上的观点是建议任何一种方法都有其优点，并且可以产生可行的结果。